The coordinates of the centre of mass of a system of three particles of mass 1g,2g and 3g are (2,2,2). Where should a fourth particle of mass 4 g be positioned so that the centre of mass of the four particle system is at the origin of the three-dimensional coordinate system ?
To solve the problem of finding the position of the fourth particle such that the center of mass of the four-particle system is at the origin, we can follow these steps:
Step 1: Understand the center of mass formula
The center of mass (CM) of a system of particles is given by the formula:
CM=∑miri∑mi
where mi is the mass of each particle and ri is the position vector of each particle.
Step 2: Calculate the total mass of the existing particles
We have three particles with masses:
- m1=1g
- m2=2g
- m3=3g
The total mass M of these three particles is:
M=m1+m2+m3=1+2+3=6g
Step 3: Determine the position of the existing center of mass
The coordinates of the center of mass of these three particles are given as (2,2,2).
Step 4: Introduce the fourth particle
Let the mass of the fourth particle be m4=4g and its position be (x,y,z).
Step 5: Set up the equation for the center of mass of the four particles
We want the center of mass of all four particles to be at the origin (0,0,0). Thus, we set up the equations for the x, y, and z coordinates:
m1⋅x1+m2⋅x2+m3⋅x3+m4⋅xM+m4=0
Substituting the values:
1⋅2+2⋅2+3⋅2+4⋅x6+4=0
Step 6: Solve for x
Calculating the left side:
2+4+6+4x10=0
This simplifies to:
12+4x=0
Solving for x:
4x=−12⇒x=−3
Step 7: Repeat for y and z coordinates
Since the center of mass coordinates are the same for y and z, we can use the same calculations for y and z:
y=−3,z=−3
Conclusion
The position of the fourth particle should be (−3,−3,−3).
Summary of the Solution
The fourth particle of mass 4g should be positioned at the coordinates (−3,−3,−3) to ensure that the center of mass of the four-particle system is at the origin.
---
The center of mass (CM) of a system of particles is given by the formula:
We have three particles with masses:
- m1=1g
- m2=2g
- m3=3g
The coordinates of the center of mass of these three particles are given as (2,2,2).
Let the mass of the fourth particle be m4=4g and its position be (x,y,z).
We want the center of mass of all four particles to be at the origin (0,0,0). Thus, we set up the equations for the x, y, and z coordinates:
Calculating the left side:
Since the center of mass coordinates are the same for y and z, we can use the same calculations for y and z:
The position of the fourth particle should be (−3,−3,−3).
The fourth particle of mass 4g should be positioned at the coordinates (−3,−3,−3) to ensure that the center of mass of the four-particle system is at the origin.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem
24 Videos
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice
90 Videos
- PROPERTIES OF SOLIDSBOOK - SL ARORACHAPTER - PROPERTIES OF SOLIDSEXERCISE - All Questions
97 Videos
- System of particles & rotational MotionBOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE
353 Videos
Similar Questions
The centre of mass of three particles of masses 1kg,2kg and 3kg lies at the point (3m, 3m, 3m). Where should a fourth particle of mass 4 kg be positioned so that the centre of mass of the four particle system lies at the point (1m, 1m, 1m)?
View SolutionThe centre of mass of three particles of masses 1kg,2kgand3kg lies at the point (3m,3m,3m) where should a fourth particles of mass 4kg be positioned so that centre of mass of the four particle system at (1m,1m,1m)?
View Solution
Knowledge Check
The centre of mass of two particles system lies
Aat the midpoint on the line joining the two particles.Bat one end of line joining the two particlesCon the line perpendicular to the line joining two particlesDon the line joining the two particlesIf the centre of mass of three particles of masses of 1kg,2kg,3kg is at (2,2,2), then where should a fourth particle of mass 4kg be placed so that the combined centre of mass may be at (0,0,0).
A(-3,-3,-3)B(3,3,3)C(-1,-2,-3)DNONE OF THESEThe centre of mass of a system of particles does not depend on
AMasses of the particlesBForces on the particles,CPosition of the particlesDRelative distance between the particles.
The coordinates of centre of mass of three particles of masses 1 kg, 2 kg, 3 kg are (2m, 2m, 2m). Where should a fourth particle of mass 4 kg be placed so that the coordinates of centre of mass are (4m, 4m, 4m)?
View SolutionThe coordinate of the centre of mass of a system as shown in figure : -
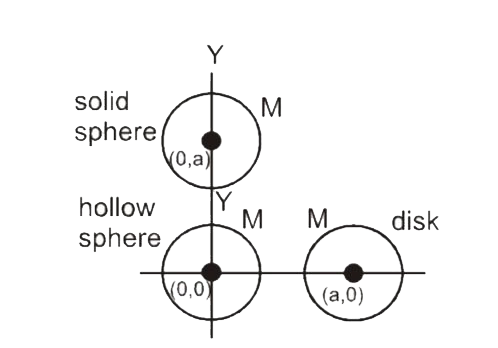
View SolutionThe coordinate of the centre of mass of a system as shown in figure : -
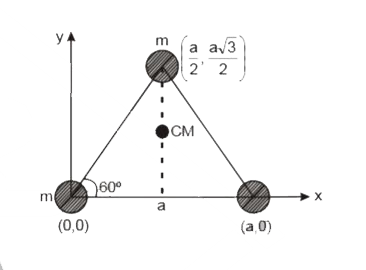
View SolutionFind out the position of centre of mass of two particle system.
View SolutionThe centre of mass of a system of particles does not depend on
View Solution
