A particle describes a horizontal circle on the smooth surface of an inverted cone. The height of the plane of the circle aove the vertex is 9.8 cm. Find the speed of the particle. Take g=9.8ms−2.
To solve the problem of finding the speed of a particle moving in a horizontal circle on the smooth surface of an inverted cone, we can follow these steps:
Step 1: Understand the Forces Acting on the Particle
The particle experiences two main forces:
- The gravitational force acting downward, which is mg.
- The normal force R acting perpendicular to the surface of the cone.
Step 2: Analyze the Geometry of the Cone
Given that the height of the circle above the vertex of the cone is h=9.8 cm, we can convert this to meters:
h=9.8cm=0.098m
Step 3: Set Up the Forces
From the geometry of the cone, we can relate the angle θ of the cone to the height h and the radius r of the circular path:
- The vertical component of the normal force balances the weight:
Rcosθ=mg
- The horizontal component provides the necessary centripetal force for circular motion:
Rsinθ=mv2r
Step 4: Divide the Two Equations
Dividing the second equation by the first gives:
RsinθRcosθ=mv2rmg
This simplifies to:
tanθ=v2rg
Step 5: Relate h, r, and θ
From the geometry of the cone, we have:
tanθ=hr
Thus, we can equate the two expressions for tanθ:
hr=v2rg
This simplifies to:
h=v2g
Step 6: Solve for the Speed v
Rearranging the equation gives:
v2=gh
Taking the square root:
v=√gh
Step 7: Substitute the Values
Substituting g=9.8m/s2 and h=0.098m:
v=√9.8×0.098
Calculating this gives:
v=√0.9604≈0.98m/s
Final Answer
The speed of the particle is approximately 0.98m/s.
---
The particle experiences two main forces:
- The gravitational force acting downward, which is mg.
- The normal force R acting perpendicular to the surface of the cone.
Given that the height of the circle above the vertex of the cone is h=9.8 cm, we can convert this to meters:
h=9.8cm=0.098m
From the geometry of the cone, we can relate the angle θ of the cone to the height h and the radius r of the circular path:
- The vertical component of the normal force balances the weight:
Rcosθ=mg
- The horizontal component provides the necessary centripetal force for circular motion:
Rsinθ=mv2r
Dividing the second equation by the first gives:
RsinθRcosθ=mv2rmg
This simplifies to:
tanθ=v2rg
From the geometry of the cone, we have:
tanθ=hr
Thus, we can equate the two expressions for tanθ:
hr=v2rg
This simplifies to:
h=v2g
Rearranging the equation gives:
v2=gh
Taking the square root:
v=√gh
Substituting g=9.8m/s2 and h=0.098m:
v=√9.8×0.098
Calculating this gives:
v=√0.9604≈0.98m/s
The speed of the particle is approximately 0.98m/s.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice
90 Videos
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice
90 Videos
- PROPERTIES OF SOLIDSBOOK - SL ARORACHAPTER - PROPERTIES OF SOLIDSEXERCISE - All Questions
97 Videos
- System of particles & rotational MotionBOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE
353 Videos
Similar Questions
A particle describes a horizontal circle of radius r on the smooth surface of an inverted cone as shown. The height of plane of circle above vertex is h. The speed of particle should be
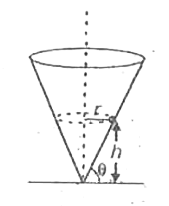
View SolutionA particle describes a horizontal circule on the smooth inner surface of a coincal funnel as shown in Fig. If the height of the plane of the circle above the vertex is 9.8cm, find the speed of the particle.
View Solution
Knowledge Check
A small ball describes a horizontal circle on the smooth inner surface of a conical funnel. If the height of the plane of the circle above vertex be 10 cm, what is the speed of the particle ?
A2 m/sB4 m/sC16 m/sD1 m/sA small ball describes a horizontal circle on the smooth inner surface of a conical funnel. If the height of the plane of the circle above vertex be 10 cm, what is the speed of the particle ?
A2 m/sB4 m/sC16 m/sD1 m/sA small ball descibes a horozontal circle on the smooth inner surface of a conical funnel. If the height of the plane of the circle above the vertex be 10 cm what is the speed of the particle?
A2 m/sB4 m/sC16 m/sD1 m/s
A particle describes a horizontal circle on smooth inner surface of a conical funnel as shown. If the height of the plane of the circle. Above the vertax is 10cm, find the speed of the paricle.
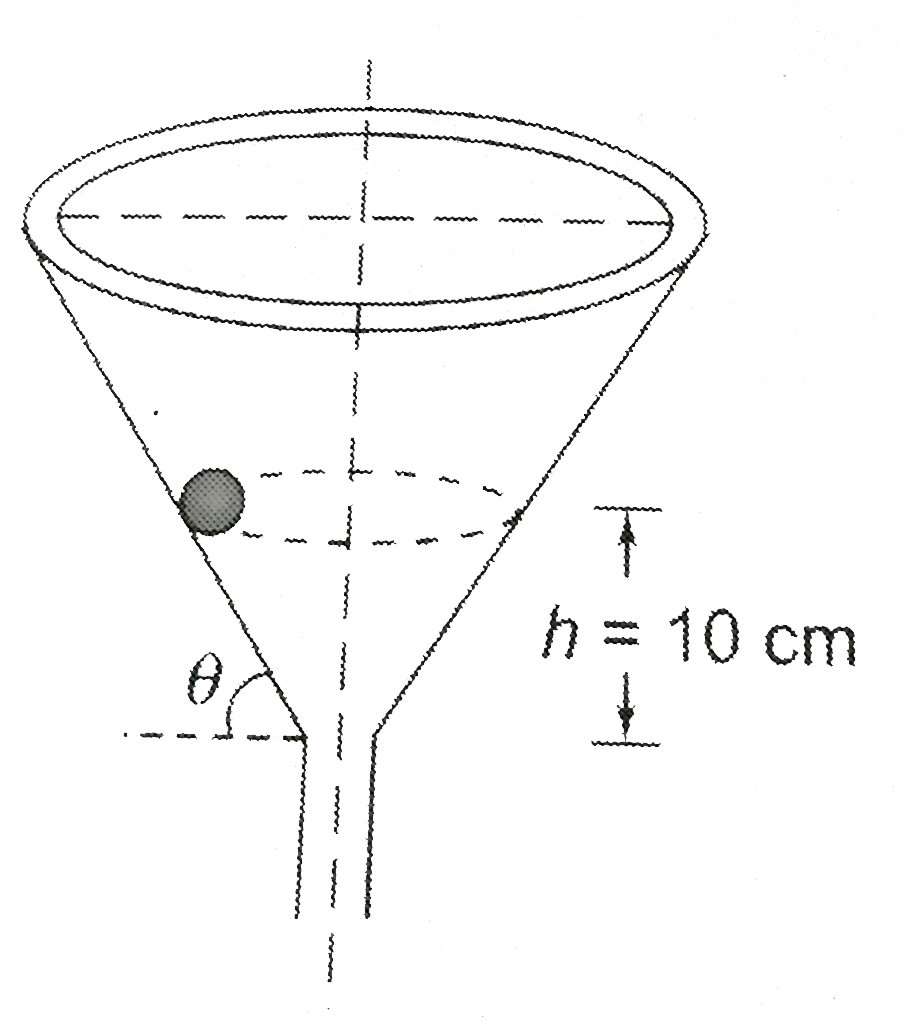
View SolutionA particle describes a horizontal circle on the smooth inner surface of a conical funnel as shown in figure - 3.44. If the height of the plane of the circle above the vertex is 9.8 cm, find the speed of the particle.
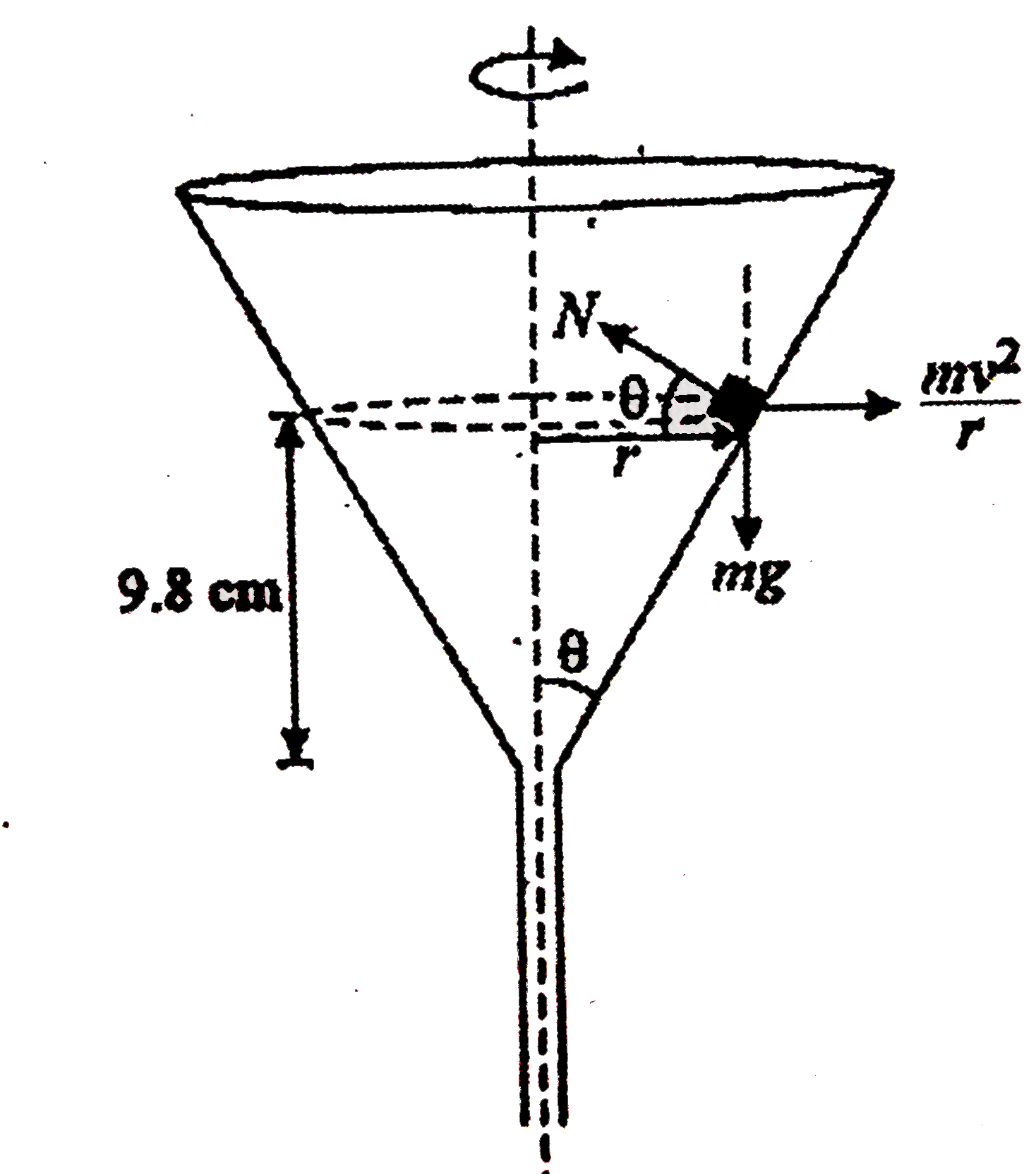
View SolutionA particle of mass 2 kg is on a smooth horizontal table and moves in a circular path of radius 0.6 m . The height of the table from the ground is 0.8 m . If the angular speed of the particle is 12rads−1 . Find the magnitude of its angular momentum about a point on the ground right under the centre of the circle .
View SolutionA particle describes a horizontal circle in a conical funnel whose inner surface is smooth with speed of 0.5m/s . What is the height of the plane of circle from vertex the funnel?
View SolutionA particle is describing circular motion in a horizontal plane in contact with the smooth surface of a fixed rigid circular cone with its axis vertical and vertex down. The height of the plane of motion above the vertex is h and the semi-vertical angle of the cone is α The period of revolution of the particle

View Solution
