Consider the following equilibrium
N2O4(g)⇔2NO2(g)
Then the select the correct graph , which shows the variation in concentratins of N2O4 Against concentrations of N2O_(4):
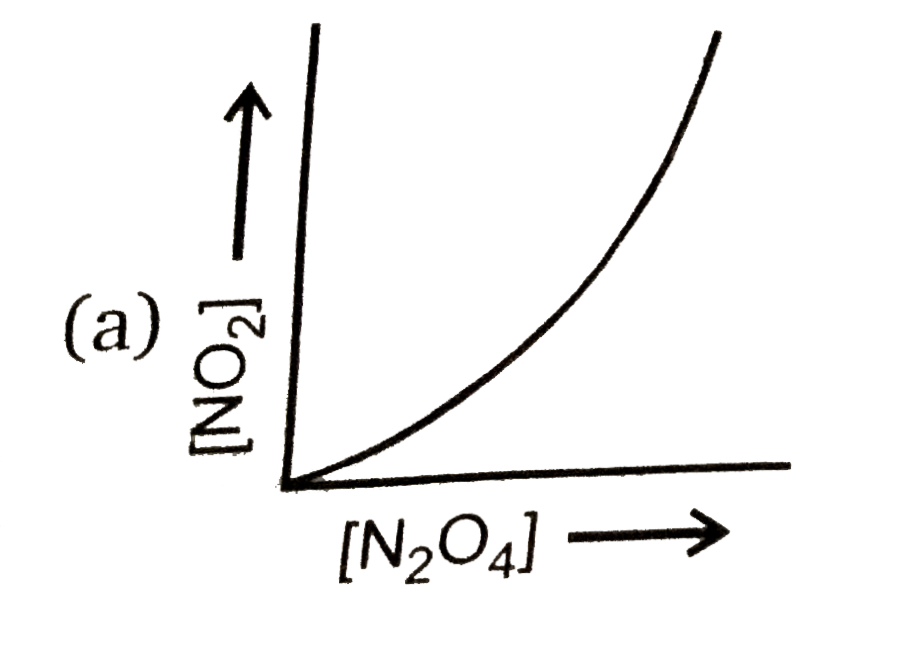
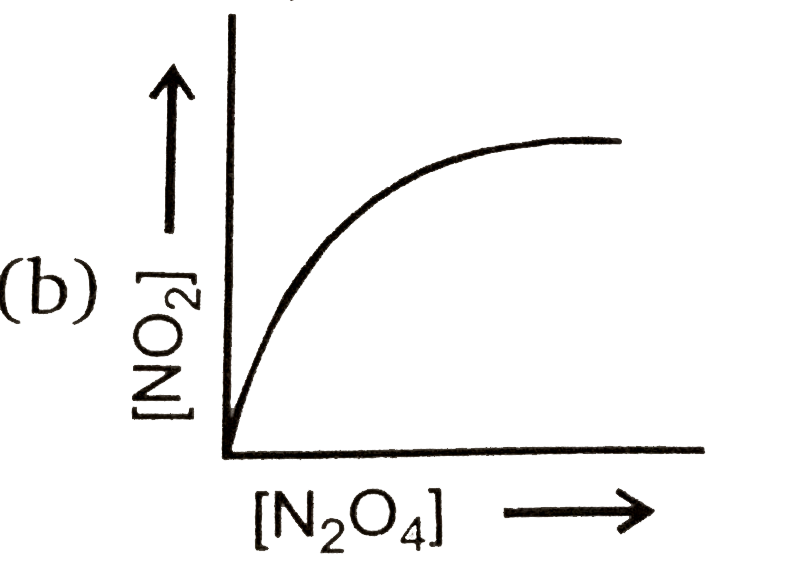
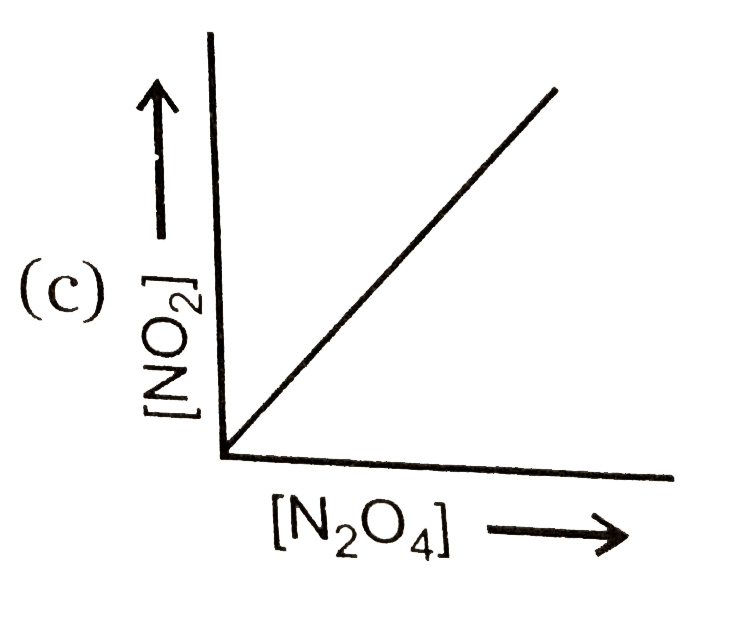
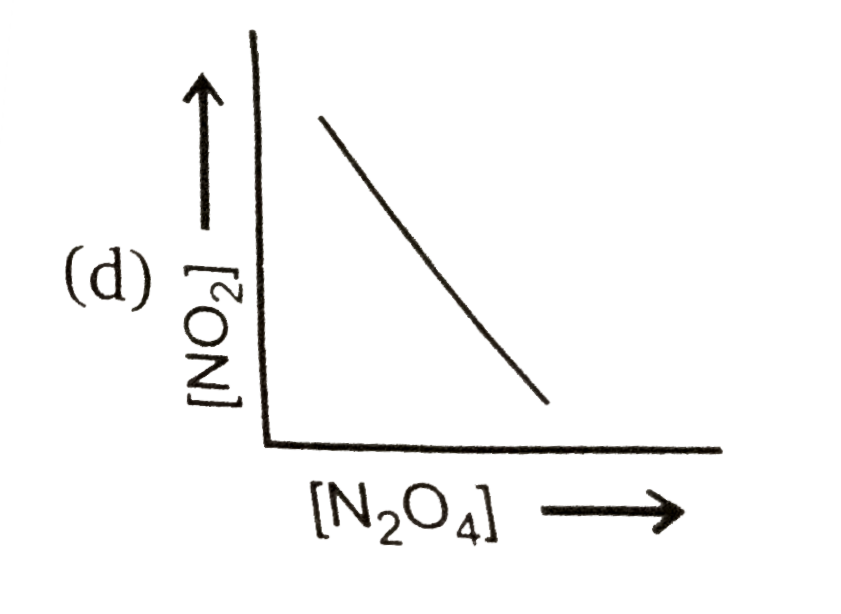
The correct Answer is:b
To solve the problem, we need to analyze the equilibrium reaction given:
N2O4(g)⇌2NO2(g)
We are tasked with determining the correct graph that shows the variation in concentrations of N2O4 against the concentrations of NO2.
1. Understanding the Reaction:
- The reaction shows that one mole of N2O4 dissociates to form two moles of NO2.
- This implies that as the concentration of N2O4 decreases, the concentration of NO2 increases.
2. Setting Up the Equilibrium Expression:
- The equilibrium constant Kc for the reaction can be expressed as:
Kc=(NO2)2(N2O4)
- Rearranging this gives:
(NO2)2=Kc⋅(N2O4)
3. Graphing the Relationship:
- In the equation (NO2)2=Kc⋅(N2O4), we can see that if we let y=(NO2) and x=(N2O4), we can rewrite it as:
y2=Kc⋅x
- This is a quadratic equation in terms of y, which indicates that the graph will be a parabola.
4. Determining the Orientation of the Parabola:
- The equation y2=Kc⋅x suggests that as x (the concentration of N2O4) increases, y2 (the square of the concentration of NO2) also increases.
- Therefore, the graph opens upwards, indicating that y increases as x increases.
5. Identifying the Correct Graph:
- Since we are looking for a graph that represents a parabolic relationship where y2 is proportional to x, and it opens upwards, we can eliminate options that show a downward-opening parabola.
- The correct graph will show a curve that starts at the origin and rises as (N2O4) increases.
Conclusion:
The correct graph is the one that represents a parabolic curve opening upwards, indicating that as the concentration of N2O4 increases, the concentration of NO2 also increases.
- The reaction shows that one mole of N2O4 dissociates to form two moles of NO2.
- This implies that as the concentration of N2O4 decreases, the concentration of NO2 increases.
- The equilibrium constant Kc for the reaction can be expressed as:
Kc=(NO2)2(N2O4)
- Rearranging this gives:
(NO2)2=Kc⋅(N2O4)
- In the equation (NO2)2=Kc⋅(N2O4), we can see that if we let y=(NO2) and x=(N2O4), we can rewrite it as:
y2=Kc⋅x
- This is a quadratic equation in terms of y, which indicates that the graph will be a parabola.
- The equation y2=Kc⋅x suggests that as x (the concentration of N2O4) increases, y2 (the square of the concentration of NO2) also increases.
- Therefore, the graph opens upwards, indicating that y increases as x increases.
- Since we are looking for a graph that represents a parabolic relationship where y2 is proportional to x, and it opens upwards, we can eliminate options that show a downward-opening parabola.
- The correct graph will show a curve that starts at the origin and rises as (N2O4) increases.
The correct graph is the one that represents a parabolic curve opening upwards, indicating that as the concentration of N2O4 increases, the concentration of NO2 also increases.
Topper's Solved these Questions
- BOOK - NARENDRA AWASTHICHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Level 1 (Q.93 To Q.122)1videos
CHEMICAL EQUILIBRIUM
- BOOK - NARENDRA AWASTHICHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Level 21videos
CHEMICAL EQUILIBRIUM
- BOOK - NARENDRA AWASTHICHAPTER - ATOMIC STUCTUREEXERCISE - Exercise273videos
ATOMIC STUCTURE
- BOOK - NARENDRA AWASTHICHAPTER - DILUTE SOLUTIONEXERCISE - Level 3 - Match The Column1videos
DILUTE SOLUTION
Similar Questions
9.2gm of N2O4 (g) is taken is a closed one litre vessel and heated till the following equilibrium is reached N2O4(g) ↔ 2NO2(g) . At equilibrium 50% of N2O4(g) is dissociated. What is the equilibrium constant (in mole lit−1 ) ?.(M.wt.of N2O4 is 92)
View SolutionThe reaction , N2O4(g)→2NO2(g) , is first order reaction , which of the following best describes the variation of concentration of N2O4 with time ?
View Solution
Knowledge Check
- Question 1 - Select One
For the following equilibrium
N2O4(g)⇔2NO2(g)
Kp is found to be equal to Kc. This is attained when :AT=1KBT=12.18KCT=27.3KDT=273K - Question 2 - Select One
For the following gases equilibrium, N2O4(g)⇔2NO2(g)
Kp is found to be equal to KP. This is attained when:A80∘CB273KC10.5KD12.19K - Question 3 - Select One
For the reaction N2O4(g)→2NO2(g)
AΔH>ΔEBΔH<ΔECΔH=ΔEDΔH=0
At the equilibrium of the reaction ,
N2O4(g)⇒2NO2(g), the observed molar mass of N2O4 is 77.70 g . The percentage dissociation of N2O4 is :-View SolutionFor the following equilibrium in gaseous phase,
N2O4⇔2NO2
NO2 is 50% of the total volume, when equilibrium is set up. Hence, percent dissociation of N2O4 is :View SolutionAt the equilibrium of the reaction ,
N2O4(g)⇒2NO2(g), the observed molar mass of N2O4 is 77.70 g . The percentage dissociation of N2O4 is :-View SolutionFor the equilibrium reaction
2NO2(g)⇔N2O4(g) + 60.0 kJ the increase in temperatureView Solution9.2 grams of N2O4(g) is taken in a closed one litre vessel and heated till the following equilibrium is reached N2O4(g)⇔2NO2(g). At equilibrium, 50%N2O4(g) is dissociated. What is the equilibrium constant (in mol litre−1) (Moleculatr weight of N2O4=92) ?
View Solution

