One of the important approach of the study of real gases involves the analysis of a parameter Z called the compressibility factor Z=PVmRT where P is pressure, Vm is molar volume ,T is absolute temperature and R is the universal gas constant .Such a relation can also be expressed as Z=(V m realVm ideal) (where Vm ideal and V_("m real") are the moler volume for ideal and real gas respectively tendencies among constituent particles.As pressure is force among is lowered or temperature is increased the value of Z approaches ideal behaviour
Choose the conslusions which are appropriate for the observation stated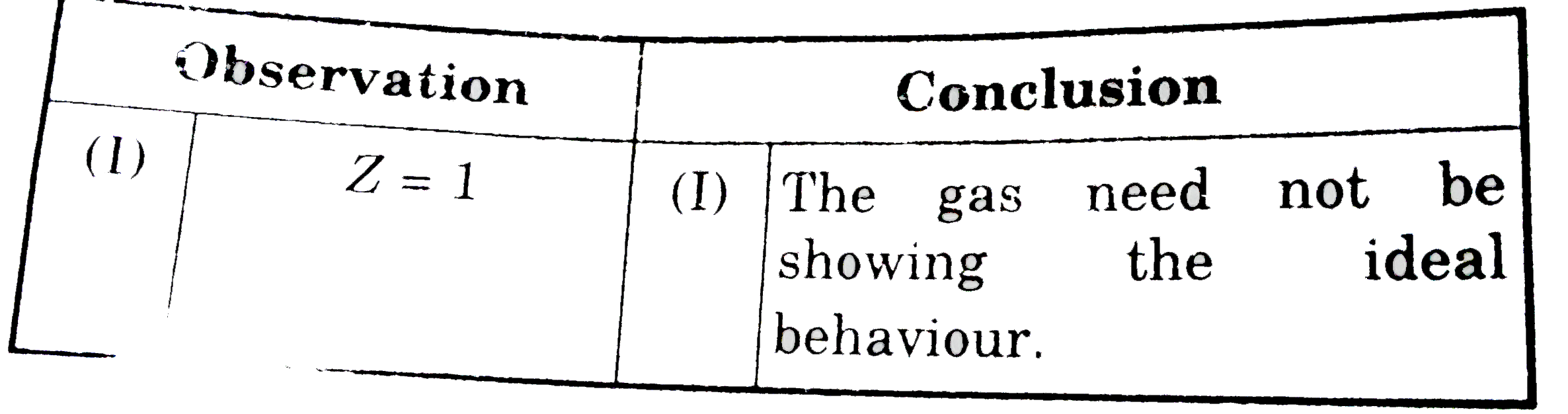 
All conclusions are true
Conclusions I, II and IV are ture
Conclusions I,III and IV are true
Cinclusions III and Iv are true
The correct Answer is:D
Topper's Solved these Questions
- GRAPHICAL INTERPRETATIONBOOK - GRB PUBLICATIONCHAPTER - GRAPHICAL INTERPRETATIONEXERCISE - Comprehension 5
1 Videos
- GRAPHICAL INTERPRETATIONBOOK - GRB PUBLICATIONCHAPTER - GRAPHICAL INTERPRETATIONEXERCISE - Comprehension 6
1 Videos
- GRAPHICAL INTERPRETATIONBOOK - GRB PUBLICATIONCHAPTER - GRAPHICAL INTERPRETATIONEXERCISE - Comprehension 3
1 Videos
- F-BLOCK ELEMENTSBOOK - GRB PUBLICATIONCHAPTER - F-BLOCK ELEMENTSEXERCISE - Subjective type
7 Videos
- HYDROCARBON (ALIPHATIC)BOOK - GRB PUBLICATIONCHAPTER - HYDROCARBON (ALIPHATIC)EXERCISE - Previous years jee questions
28 Videos
Similar Questions
One of the important approach to the study of real gases involves the analysis of parameter Z called the compressibility factor Z=PVmRT where P is pressure, Vm is molar volume, T is absolute temperature and R is the universal gas constant. such a relation can also be expressed as Z=(VmrealVmal) (where Vmal and Vmreal are the molar volume for ideal and real gas respectively). Gas corresponding Z<1 have attractive forces amoung constituent particles. As the pressure is lowered or temperature is increased the value of Z approaches 1. (reaching the ideal behaviour)
For a real gas GZ>1 at STP Then for 'G': Which of the following is true:
View SolutionOne of the important approach to the study of real gases involves the analysis of parameter Z called the compressibility factor Z=PVmRT where P is pressure, Vm is molar volume, T is absolute temperature and R is the universal gas constant. such a relation can also be expressed as Z=(VmrealVmal) (where Vmal and Vmreal are the molar volume for ideal and real gas respectively). Gas corresponding Z<1 have attractive forces amoung constituent particles. As the pressure is lowered or temperature is increased the value of Z approaches 1. (reaching the ideal behaviour)
ObservationConclusionI.Z=1I.The gas need not be showing the ideal behaviourII.Z>1II.On applying pressure the gas will respond byincreasing its volumeIII.Z<1III.The gas may be liquefiedIV.Z→1for lowPIV.The gas is approaching the ideal behaviour
View Solution
Knowledge Check
One of the important approach of the study of real gases involves the analysis of a parameter Z called the compressibility factor Z=PVmRT where P is pressure, Vm is molar volume ,T is absolute temperature and R is the universal gas constant .Such a relation can also be expressed as Z=(V m realVm ideal) (where Vm ideal and V_("m real")arethemo≤rvolumeforalandrealgasrespectivelytendenciesamongconstituentpartic≤s.Aspressureisforceamongisloweredortemperatureis∈creasedthevalueofZapproachesalbehaviour<br>Forarealgas'G',Zgt1 at STP, then for 'G' which of the following is true ?
A1mole of the gas occupies 22.7 L at STPB1 mole of the gas occupies 22.7 L at pressure higher then that at STP (Keeping temperature constant )C1 Mole of the gas occupies 22.7 L at pressure lower then that at STP (keeping temperature constant )DNone of the aboveOne of the important approach of the study of real gases involves the analysis of a parameter Z called the compressibility factor Z=PVmRT where P is pressure, Vm is molar volume ,T is absolute temperature and R is the universal gas constant .Such a relation can also be expressed as Z=(V m realVm ideal) (where Vm ideal and V_("m real") are the moler volume for ideal and real gas respectively tendencies among constituent particles.As pressure is force among is lowered or temperature is increased the value of Z approaches ideal behaviour
Following graph represents a pressure (P) volume (V) relationship at a fixed temperature (T) for moles of a real gas.The graph has two regions masked (I) and (II). Which of the folloing option true ?
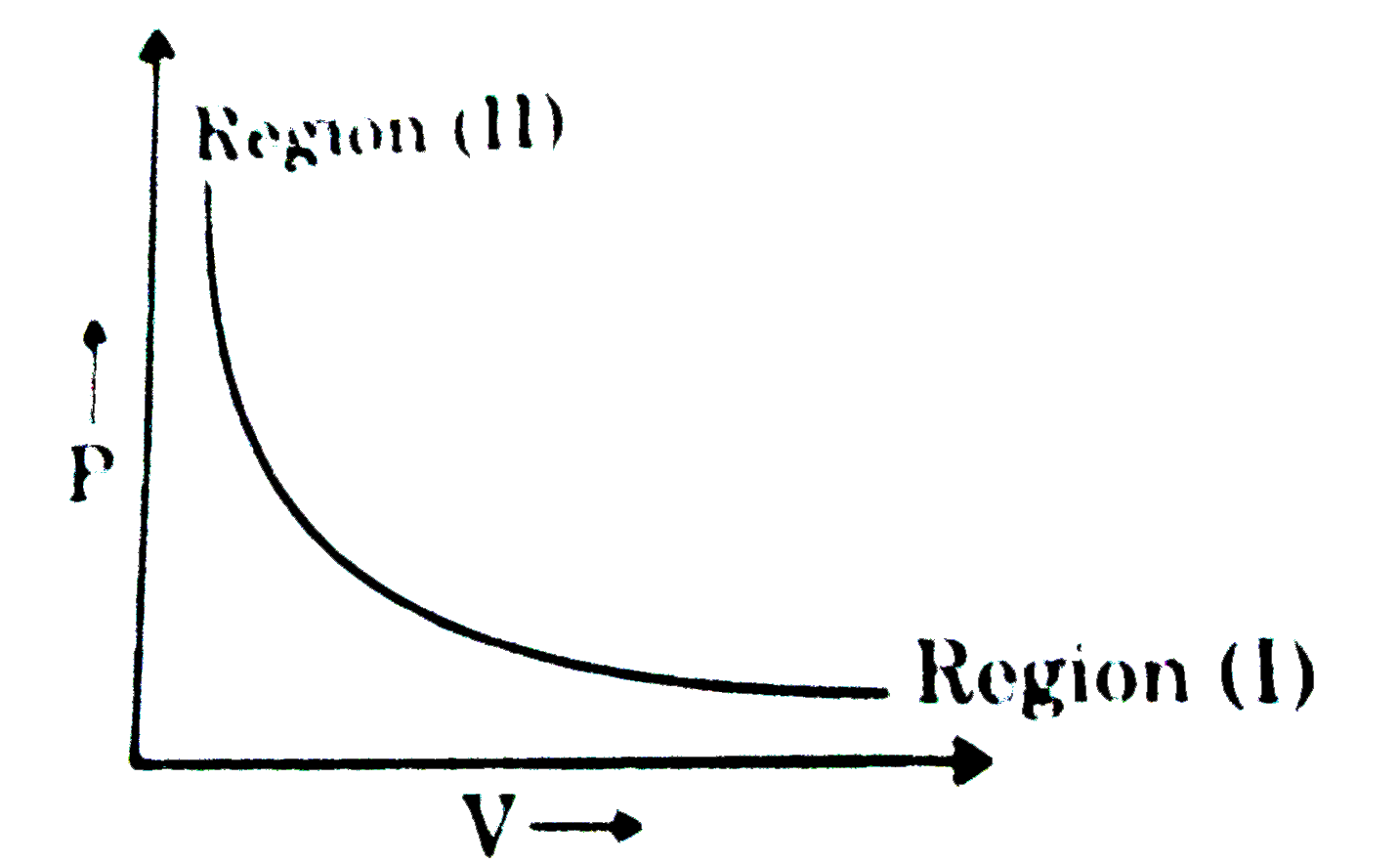AZ<1 in the region (II)BZ = 1 in the region (II)CZ = 1 for the curveDZ approaches 1 as we move from region (II) region(I)One of the important approach to the study of real gases involves the analysis of parameter Z called the compressibility factor Z=PVmRT where P is pressure, Vm is molar volume, T is absolute temperature and R is the universal gas constant. such a relation can also be expressed as Z=(VmrealVmal) (where Vmal and Vmreal are the molar volume for ideal and real gas respectively). Gas corresponding Z<1 have attractive forces amoung constituent particles. As the pressure is lowered or temperature is increased the value of Z approaches 1. (reaching the ideal behaviour)
Following graph represents a pressure (P) volume (V) relationship at a fixed temperature (T) for n moles of a real gas. The graph has two regions marked (I) and (II). Which of the following options is true.
AZ<1 in the region (II)BZ=1 I the region (II)CZ=1 for the curveDZ approaches 1 as we move from region (II) to region (I)
The equation of state of a real gas is given by (P+aV2)(V−b)=RT
where P, V and T are pressure, volume and temperature resperature and R is the universal gas constant. The dimensions of the constant a in the above equation is
View SolutionThe equation of state of a real gas is given by (P+aV2)(V−b)=RT
where P, V and T are pressure, volume and temperature resperature and R is the universal gas constant. The dimensions of the constant a in the above equation is
View SolutionOne of the important approach to the study of real gases involves the analysis of parameter Z called the compressibility factor Z=PVmRT where P is pressure, Vm is molar volume, T is absolute temperature and R is the universal gas constant. such a relation can also be expressed as Z=(VmrealVmal) (where Vmal and Vmreal are the molar volume for ideal and real gas respectively). Gas corresponding Z<1 have attractive forces amoung constituent particles. As the pressure is lowered or temperature is increased the value of Z approaches 1. (reaching the ideal behaviour)
For a real gas GZ>1 at STP Then for 'G': Which of the following is true:
View SolutionOne of the important approach to the study of real gases involves the analysis of parameter Z called the compressibility factor Z=PVmRT where P is pressure, Vm is molar volume, T is absolute temperature and R is the universal gas constant. such a relation can also be expressed as Z=(VmrealVmal) (where Vmal and Vmreal are the molar volume for ideal and real gas respectively). Gas corresponding Z<1 have attractive forces amoung constituent particles. As the pressure is lowered or temperature is increased the value of Z approaches 1. (reaching the ideal behaviour)
ObservationConclusionI.Z=1I.The gas need not be showing the ideal behaviourII.Z>1II.On applying pressure the gas will respond byincreasing its volumeIII.Z<1III.The gas may be liquefiedIV.Z→1for lowPIV.The gas is approaching the ideal behaviour
View SolutionOne of the approach to the study of real gases involves the analysis of a parameter Z called the compressibility factor Z=PVmRT where P is pressure, Vm is molar volume, T is absolute temperature and R is the universal gas constant . Such a relation can also be expressed as Z=(Vm realVm ideal) (where Vm ideal and Vm real are the molar volume for ideal and real gas respectively) . Gas corresponding Z>1 have repluive tendenciesamong constituent particles due to their size factor, among constitutent particles . As the pressure is lowered or temperature is increased the value of Z approaches 1. ( reaching the ideal behaviour)
For a real gas 'G'Z>1 at STP then for 'G' which of the following is true
View Solution