A solid sphere of radius R is charged uniformly. The electrostatic potential V is plotted as a function of distance r from the centre of th sphere. Which of the following best represents the resulting curve?

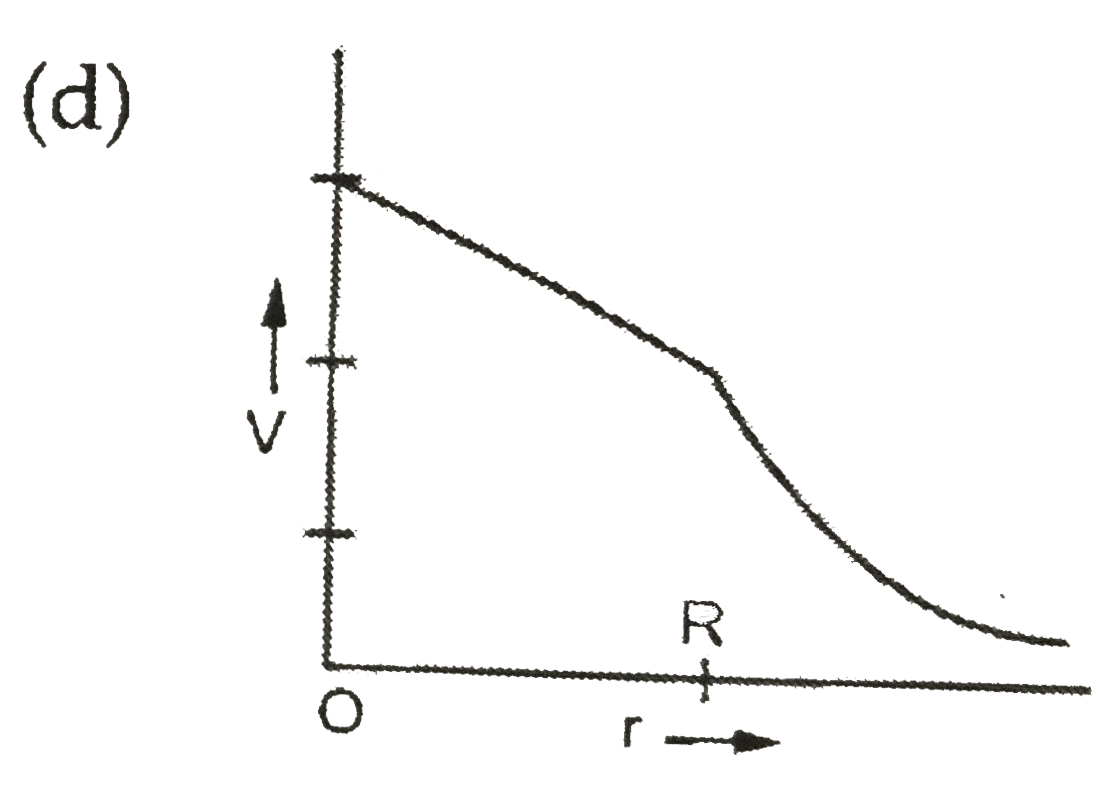
The correct Answer is:C
To solve the problem of how the electrostatic potential V varies as a function of distance r from the center of a uniformly charged solid sphere, we can break down the analysis into several steps:
1. Understanding the Charge Distribution:
- A solid sphere of radius R is uniformly charged. This means that the charge Q is distributed evenly throughout the volume of the sphere.
2. Electrostatic Potential Inside the Sphere:
- For a point inside the sphere (where r<R), the electrostatic potential V can be expressed as:
V=kQ2R(3−r2R2)
- Here, k is Coulomb's constant, and r is the distance from the center of the sphere.
3. Electrostatic Potential at the Surface of the Sphere:
- At the surface of the sphere (where r=R), the potential can be calculated as:
V(R)=kQR
4. Electrostatic Potential Outside the Sphere:
- For points outside the sphere (where r>R), the potential behaves like that of a point charge:
V=kQr
5. Behavior of the Potential:
- Inside the sphere, as r increases from 0 to R, the potential decreases from a maximum value at the center to the value at the surface.
- Outside the sphere, as r increases beyond R, the potential decreases inversely with distance.
6. Graphical Representation:
- The graph of V as a function of r will show a decrease in potential as you move from the center of the sphere to the surface and then continue to decrease as you move further away from the sphere.
- The curve will start at a maximum value at the center, decrease to a certain value at the surface, and then follow a hyperbolic decline for r>R.
7. Choosing the Correct Option:
- Based on the analysis, the correct representation of the potential V as a function of distance r from the center of the sphere is best represented by a curve that initially decreases and then follows an inverse relationship for r>R. This corresponds to option C.
Final Answer:
The best representation of the electrostatic potential V as a function of distance r from the center of the uniformly charged solid sphere is option C.
- A solid sphere of radius R is uniformly charged. This means that the charge Q is distributed evenly throughout the volume of the sphere.
- For a point inside the sphere (where r<R), the electrostatic potential V can be expressed as:
V=kQ2R(3−r2R2)
- Here, k is Coulomb's constant, and r is the distance from the center of the sphere.
- At the surface of the sphere (where r=R), the potential can be calculated as:
V(R)=kQR
- For points outside the sphere (where r>R), the potential behaves like that of a point charge:
V=kQr
- Inside the sphere, as r increases from 0 to R, the potential decreases from a maximum value at the center to the value at the surface.
- Outside the sphere, as r increases beyond R, the potential decreases inversely with distance.
- The graph of V as a function of r will show a decrease in potential as you move from the center of the sphere to the surface and then continue to decrease as you move further away from the sphere.
- The curve will start at a maximum value at the center, decrease to a certain value at the surface, and then follow a hyperbolic decline for r>R.
- Based on the analysis, the correct representation of the potential V as a function of distance r from the center of the sphere is best represented by a curve that initially decreases and then follows an inverse relationship for r>R. This corresponds to option C.
The best representation of the electrostatic potential V as a function of distance r from the center of the uniformly charged solid sphere is option C.
Topper's Solved these Questions
Similar Questions
A sphere of radius R, is charged uniformly with total charge Q. Then correct statement for electric field is (r = distance from centre): -
View SolutionA hollow metal sphere of radius 5 cm is charged such that the potential on its surface is 10V. The potential at the distance 3cm from the centre of the sphere is:
View Solution
Knowledge Check
- Question 1 - Select One
A conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
ARVr2BVRCrVR2DR2Vr2 - Question 2 - Select One
A conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
AVrBR2Vr3CRVr2DrVR2 - Question 3 - Select One
A hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
Adecreases as r increases for r<R and r>RBincreases as r increases for r<R and r>RCzero as r increases for r<R, decreases as r increases for r>RDzero as r increases for r<R, increases for r>R
A hollow metal sphere of radius 5cm is charged such that the potential on its surface is 10V. The potential at a distance of 2cm from the centre of the sphere
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View SolutionA sphere of radius R has a charge density σ. The electric intensity at a point at a distance r from its centre is
View SolutionA non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
View SolutionThe potential at a distance R/2 from the centre of a conducting sphere of radius R will be
View Solution

