There is a uniform magnetic field $B$ normal to the $x y$ plane. A conductor $A B C$ has length $A B = l_{1}$ , parallel to the $x$ axis, and lengthh $B C = l_{2}$ parallel to the $y$ -axis. $A B C$ moved in the $x y$ plane with velocity $v_{x} ˆ i + v_{y} ˆ j$ . The potential difference between $A$ and $C$ is proportional to

A

$v_{x} l_{1} + v_{y} l_{2}$

B

$v_{x} l_{2} + v_{y} l_{1}$

C

$v_{x} l_{2} - v_{y} l_{1}$

D

$v_{x} l_{1} - v_{y} l_{2}$

Text Solution

Verified by Experts

The correct Answer is:A

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
There is a uniform magnetic field $B$ normal to the $x y$ plane. A conductor $A B C$ has length $A B = l_{1}$ , parallel to the x-axis, and length $B C = l_{2}$ , parallel to the y-axis. $A B C$ moves in the xy plane with velocity $v_{x} ˆ i + v_{y} ˆ j$ . The potential difference between $A$ and $C$ is proportional to

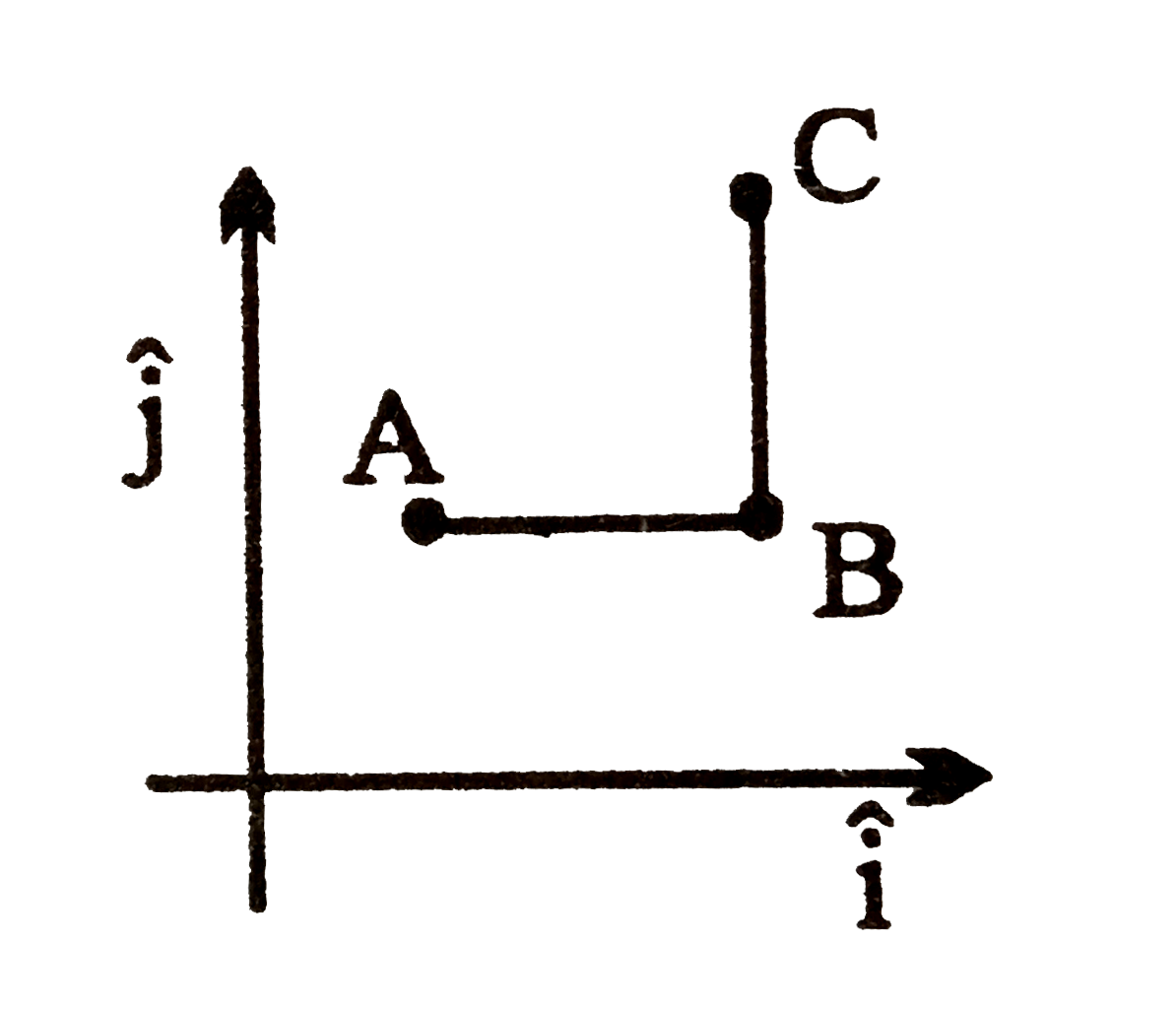A $v_{x} l_{1} + v_{y} l_{2}$
B $v_{x} l_{2} + v_{y} l_{1}$
C $v_{x} l_{2} - v_{y} l_{1}$
D $v_{x} l_{1} - v_{y} l_{2}$
Question 2 - Select One or More
The conductor ABCD has the shape shown. It lies in the yz plane, with A and e on the y-axis. When it moves with a velocity v in a magnetic field B, and emf e is induced between A and E .

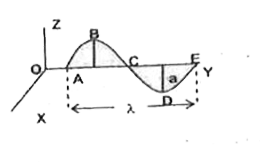Ae = 0, if v is in the y- direction and B is in the x-direction
Be = 2Bav, if v is in the z-direction and B is in the x-direction
Ce = B $λ$ v, if v is in the z- direction and B is in the x- direction
De = B $λ$ v, if v is in the x-direction and B is in the z-direction
Question 3 - Select One
A conducting rod of length l is falling with a velocity v perpendicular to a uniform horizontal magnetic field B. The potential difference between the two ends will be
A2 Blv
BBlv
C $\frac{1}{2} B l v$
D $\frac{1}{2} B l^{2} v^{2}$

D MUKHERJEE-MOTION OF CHARGED PARTICLES-All Questions

Home
Ask Doubt
Profile