
In the figure above, ¯¯¯¯¯¯¯MQ and ¯¯¯¯¯¯NR intersect at point P, NP = QP, and MP = PR. What is the measure, in degrees, of ∠QMR ? (Disregard the degree symbol when gridding your answer.)
It is given that the measure of ∠QPR is 60∘. Angle MPR and ∠QPR are collinear and therefore are supplementary angles. This means that the sum of the two angle measures is 180∘, and so the measure of ∠MPR is 120∘. The sum of the angles in a triangle is 180∘. Subtracting the measure of ∠MPR from 180∘ yields the sum of the other angles in the triangle MPR. Since 180 − 120 = 60, the sum of the measures of ∠QMR and ∠NRM is 60∘. It is given that MP = PR, so it follows that triangle MPR is isosceles. Therefore ∠QMR and ∠NRM must be congruent. Since the sum of the measure of these two angles is 60∘, it follows that the measure of each angle is 30∘.
An alternate approach would be to use the exterior angle theorem, noting that the measure of ∠QPR is equal to the sum of the measures of ∠QMR and ∠NRM. Since both angles are equal, each of them has a measure of 30∘.
Similar Questions

In the figure above, point D is on line AC, AB=BD=CD, and AD=15. What is the measure, in degrees, of ∠BCD? (Disregard the degree symbol when gridding your answer).
View SolutionA square is inscribed in a circle. The area of the square is what percent of the area of the circle? (Disregard the percent symbol when gridding your answer).
View Solution
Knowledge Check
In the figure below , x is in ¯¯¯¯¯¯¯WZ . If the angle measure are as shown , what is the degree measure of ∠YXZ?
 A25∘B3712∘C6512∘D11412∘
A25∘B3712∘C6512∘D11412∘In the figure below, A, D, C and E are collinear . ¯¯¯¯¯¯AD,¯¯¯¯¯¯BD,and¯¯¯¯¯¯BC are all the same length, and the angle measure of ∠ABD is as marked. What is the degree measure of ∠BCE?
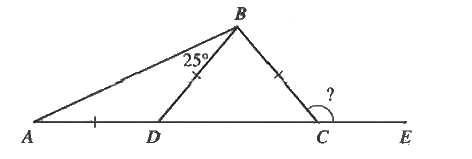 A50∘B100∘C105∘D130∘
A50∘B100∘C105∘D130∘
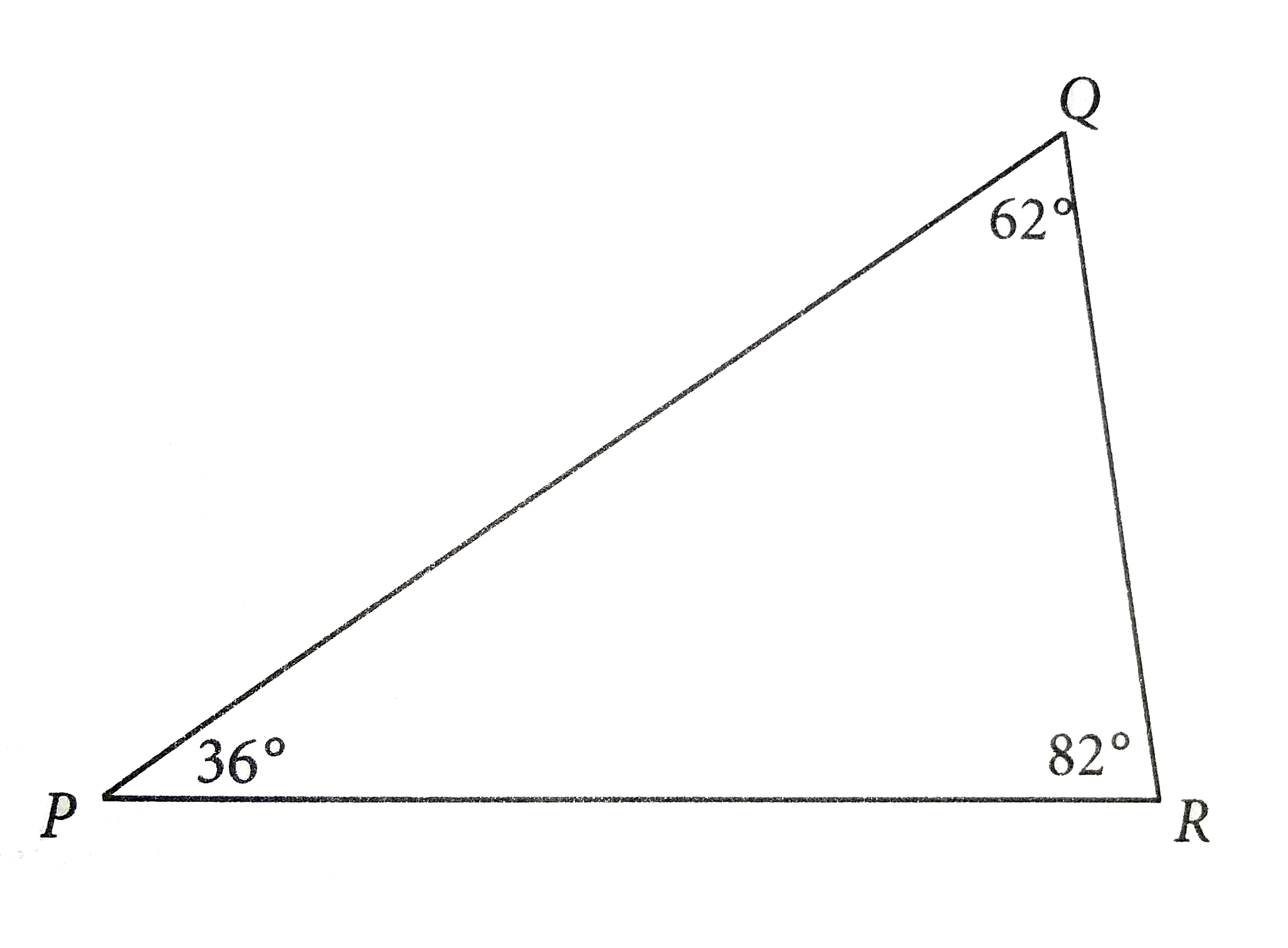
In the figure above, triangle PQR is a similar to triangle XYZ (not shown) . IF PQ:XY=QR:YZ=PR:XZ=4:5, what is the measure , in degrees, of angle Y?
View SolutionIf the diagonals AC and BD intersect at point P in the cube in Figure what is the degree measure of angle APB ?

View Solution
In the figure shown above, ∠Q measures 70∘ , ¯¯¯¯¯¯PQ≅¯¯¯¯¯¯PR , and ¯¯¯¯¯¯PQ and ¯¯¯¯¯¯PR are tangent to the circle with center O at points A and B . Find , in degrees , the measure of ∠AOB.
View SolutionWith reference to the given figure, a man stands on the ground at point A, Which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m . The man's eye is 2 m above the ground. He observes the angle of elevation of C, the top of the pole, as x∘ , where tan x∘=25 . Calculate :
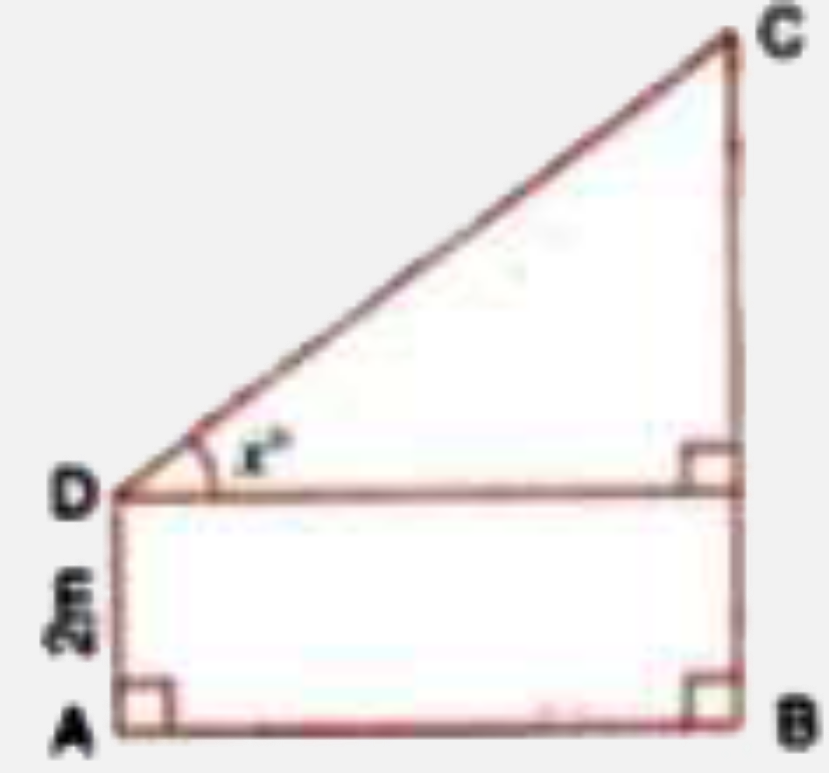
angle of elevation of the top of the pole when he is standing 15 metres from the pole. Give your answer to the nearest degree.
View SolutionAn electrometer consister of a fixed vertical metal bar OB at the top of which is attached a thin rod OA which gets deflected from the bar under the action of an electric charge (fig.). The rod can rotate in vertical plane about fixed horizontal axis passing through O. The reading is taken on a quadrant graduated in degrees. The length of the rod is l and its mass is m. what will be the charge when the rod of such an electrometer is deflected through an angle α in equilibrium. Find the answer using the following two assumptions :
The charge on the electrometer is equally distributed between the bar & the rod and the charges are concentrated at point A on the rod & at point B on the bar.

View Solution
