The number of radians in a 720-degree angle can be written as aπ, where a is a constant. What is the value of a ?
To find the value of a in the expression where the number of radians in a 720-degree angle can be written as aπ, we can follow these steps:
Step 1: Understand the conversion from degrees to radians.
We know that:
180∘=π radians
This means that to convert degrees to radians, we can use the relationship:
Radians=Degrees×π180
Step 2: Apply the conversion to 720 degrees.
Now, we need to convert 720 degrees to radians using the formula:
Radians=720∘×π180
Step 3: Simplify the expression.
Calculating the multiplication:
Radians=720×π180
Now, simplify 720180:
720180=4
Thus, we have:
Radians=4π
Step 4: Identify the value of a.
From the expression 4π, we can see that it can be written as aπ where a=4.
Final Answer:
The value of a is:
4
---
We know that:
180∘=π radians
This means that to convert degrees to radians, we can use the relationship:
Radians=Degrees×π180
Now, we need to convert 720 degrees to radians using the formula:
Radians=720∘×π180
Calculating the multiplication:
Radians=720×π180
Now, simplify 720180:
720180=4
Thus, we have:
Radians=4π
From the expression 4π, we can see that it can be written as aπ where a=4.
The value of a is:
4
Similar Questions
(7532+100y2)+10(10y2−110)
The expression above can be written in the form ay2+b, where a and b are constants. What is the value of a + b ?
View SolutionThe relationship between x and y can be written as y = mx , where m is a constant. If y = 17 when x = a , what is the value of y when x = 2a ?
View Solution
Knowledge Check
What is the angle measure of 4 radians ?
A114.591∘B141.372∘C229.183∘D282.743∘IF n is a constant equal to the number of degrees in an angle measuring 3π radians, what is the value of n?
A240B320C270D540
The sum of −2x2+x+31 and 3x2+7x−8 can be written in the form ax2+bx+c, where a, b, and c are constants.What is the value of a + b + c ?
View Solution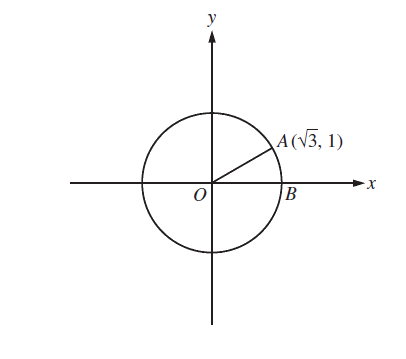
In the xy-plane above, O is the center of the circle, and the measure of ∠AOB is πa radians. What is the value of a ?
View SolutionIf the expression 2−i2+i is written as the complex number a+bi, where a and b are real numbers, then what is the value of a ? (Note: i=√−1)
View Solution
In the xy-plane above, O is the center of the circle, and the measure of angle θ is kπ radians. If 0≤θ≤2π, what is the value of k?
View SolutionAn angle in the xy-plane has measure 5π radians What is the measure of the angle in degrees?
View SolutionIf the expression −3I2+2i2+i is written in the form a+bi, where a and b are real numbers and I=√−1, what is the value of a ?
View Solution
