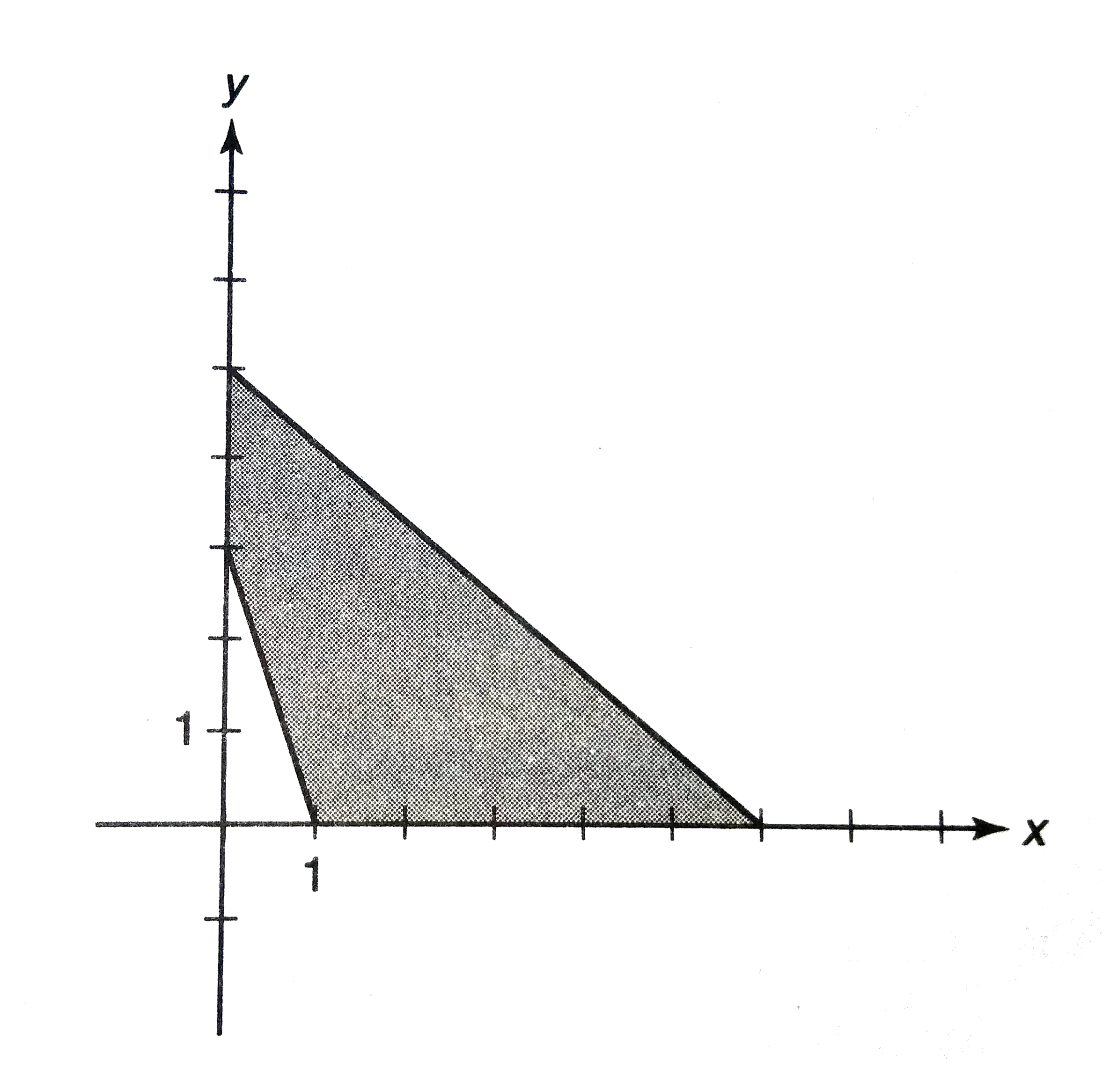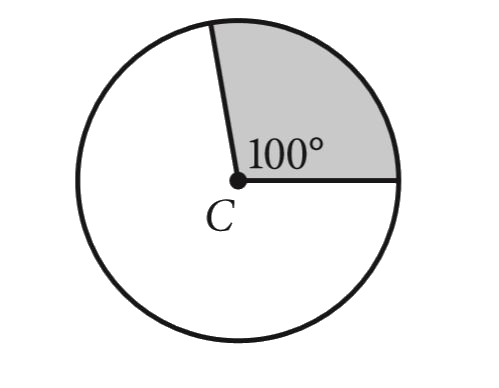
Point C is the center of the circle above. What fraction of the area of the circle is the area of the shaded region?
Video Solution
Text Solution
There are 360∘ in a circle, and it is shown that the central angle of the shaded region is 100∘. Therefore, the area of the shaded region can be represented as a fraction of the area of the entire circle, 100360 , which can be reduced to 518 . Either 5/18, .277, or .288 can be gridded as the correct answer.
|
Similar Questions
Knowledge Check
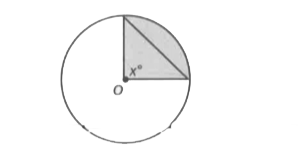
O is the center of the circle.
The area of the circle is 16π.
The area of the shaded region <4π.
Quantity AQuantity Bx90AQuantity A is greater.BQuantity B is greater.CThe two quantities are equal.DThe relationship cannot be determined from the infromation given.
Point K is the center of the circle above, and the coordinates of Point K are (2, -1). What is the area of the circle?AπB2πC4πD8πIn the figure, ABCD is a rectangle and points E, F, G and H are midpoints of its sides. What is the ratio of the area of the shaded region to the area of the un-shaded region in the rectangle?
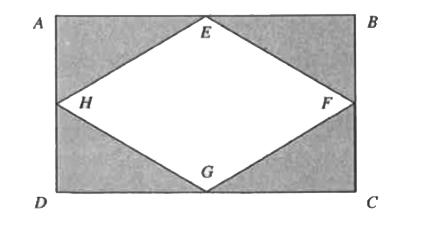 A1:1B1:2C2:1D1:3
A1:1B1:2C2:1D1:3
Find the area of the shaded region in figure.

View SolutionFind the area of the shaded region in Figure.
View SolutionThe perimeter of a circle is4πr cm. What is the area of the circle?
View SolutionIn Fig. 12.25, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.
View Solution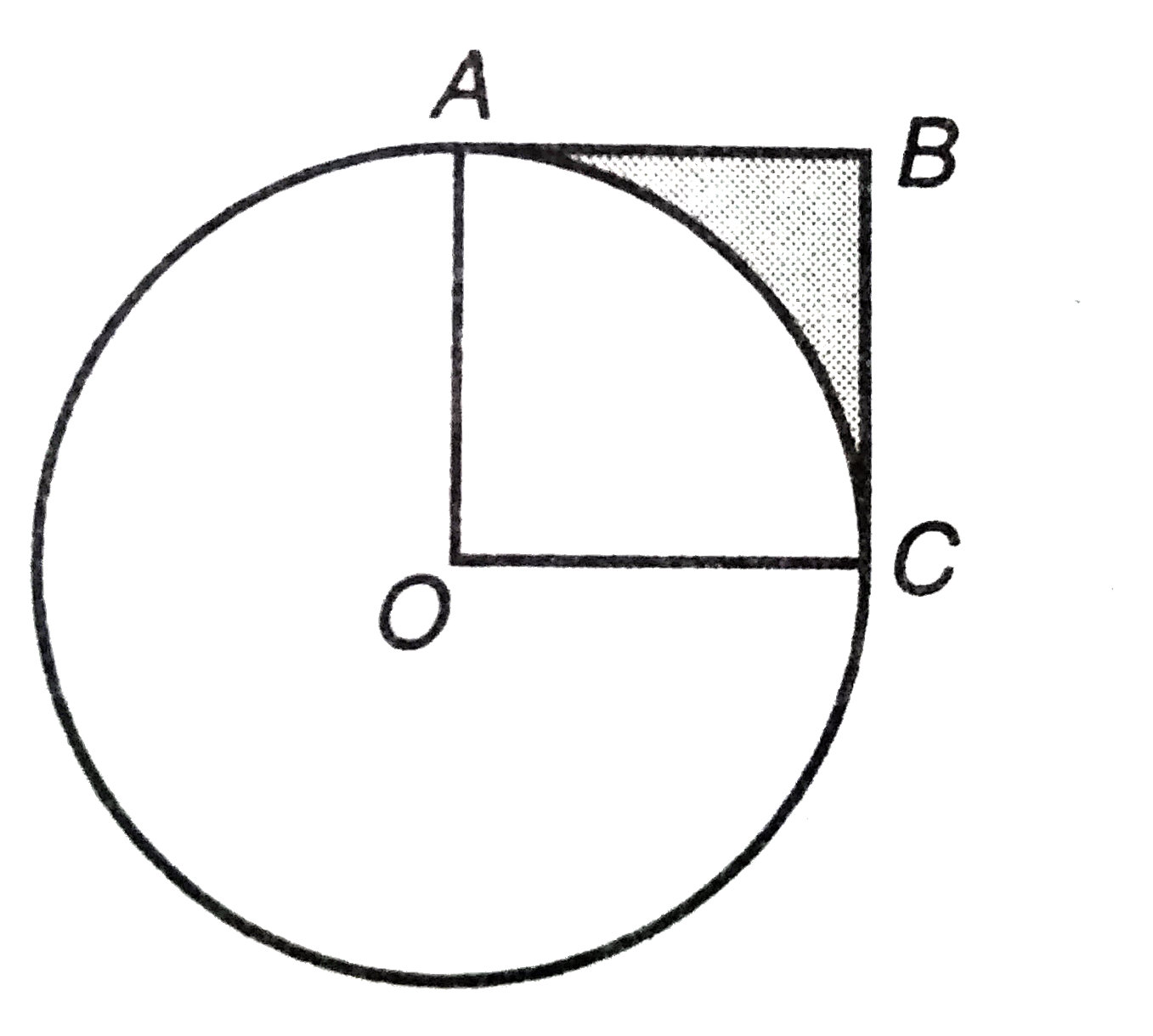
In the figure above, OABC is a square. If the area of circle O is 2π, what is the area of the shaded region?
View Solution