
In the figure above , tan B=34. If BC =15 and DA=4, what is the length of ¯¯¯¯¯¯DE ?
Since tan B = 34 , △ABC and △DBE are both 3-4-5 triangles. This means that they are both similar to the right triangle with sides of lengths 3, 4, and 5. Since BC = 15, which is 3 times as long as the hypotenuse of the 3-4-5 triangle, the similarity ratio of △ABC to the 3-4-5 triangle is 3:1. Therefore, the length of ¯¯¯¯¯¯AC (the side opposite to B) is 3 × 3 = 9, and the length of ¯¯¯¯¯¯AB (the side adjacent to angle B) is 4 × 3 = 12. It is also given that DA = 4. Since AB = DA + DB and AB = 12, it follows that DB = 8, which means that the similarity ratio of △DBE to the 3-4-5 triangle is 2:1 ( ¯¯¯¯¯¯DB is the side adjacent to angle B). Therefore, the length of ¯¯¯¯¯¯DE , which is the side opposite to angle B, is 3 × 2 = 6.
Similar Questions
The inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View SolutionWhat is the distance OA for the square shown in figure :- ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R05_E01_015_Q01.png" width="80%"gt
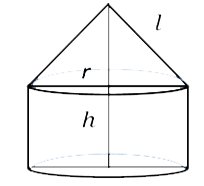
View SolutionThe total surface area of the given solid figure is _______________.
View SolutionIn the given fig. If DE||BC Find EC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/MATH_241_X_SQP_E01_021_Q01.png" width="80%"gt
View SolutionWhat is the distance OA for the square shown in figure :- ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R05_E01_015_Q01.png" width="80%"gt
View Solution
