Question

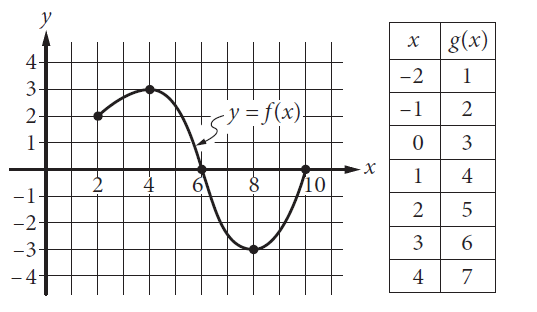
The complete graph of the function f and a table of values for the function g are shown above. The maximum value of f is k.What is the value of g(k) ?

Options

A. 7
B. 6
C. 3
D. 0

Answer

B

Explanation

The maximum value of the function f occurs at the highest point on the graph of y = f (x), the highest point on the graph is (4, 3). For any point on the graph of f, the y-coordinate gives the value of the function at the x-coordinate, therefore, the maximum value of the function f is 3. It is stated that k is the maximum value of f, so k = 3. Thus, g (k) = g (3). From the table of values for g, it can be seen that when x = 3, g (3) = 6.
Choice A is incorrect and may result from using the x-coordinate of the maximum point as the value of k. Choice C is incorrect, it is the value of k, not of g (k). Choice D is incorrect and may be the result of giving the value of x that makes g (x) = 3 instead of finding the value of g (x) when x = 3.