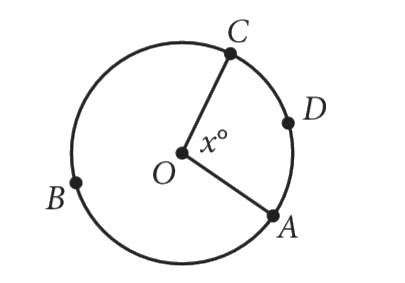
The circle above has center O, the length of arc ⌢ADC is 5π , and x=100. What is the length of arc ⌢ABC ?
9π
13π
18π
132π
The correct Answer is:B
The ratio of the lengths of two arcs of a circle is equal to the ratio of the measures of the central angles that subtend the arcs. It’s given that arc ⌢ADC is subtended by a central angle with measure 100∘. Since the sum of the measures of the angles about a point is 360∘, it follows that arc ⌢ABC is subtended by a central angle with measure 360∘−100∘=260∘. If s is the length of arc ⌢ABC , then s must satisfy the ratio s5π=260100 . Reducing the fraction 260100 to its simplest form gives 135 . Therefore, s5π = 135 . Multiplying both sides of s5π=135 by 5π yields s = 13π.
Choice A is incorrect. This is the length of an arc consisting of exactly half of the circle, but arc ⌢ABC is greater than half of the circle. Choice C is incorrect. This is the total circumference of the circle. Choice D is incorrect. This is half the length of arc ⌢ABC , not its full length.
Similar Questions

In the circle above, point A is the center and the length of arc ⌢BC is 25 of the circumference of the circle. What is the value of x ?
View SolutionPoints A and B lie on a circle with radius 1, and arc ⌢AB has length π3. What fraction of the circumference of the circle is the length of arc ⌢AB ?
View Solution
Knowledge Check
The circle below has an area of 64πcm2 .A central angle with measure 24∘ intercepts minor arc ⌢CD what is the length of minor are ⌢CD , in centimeters ?
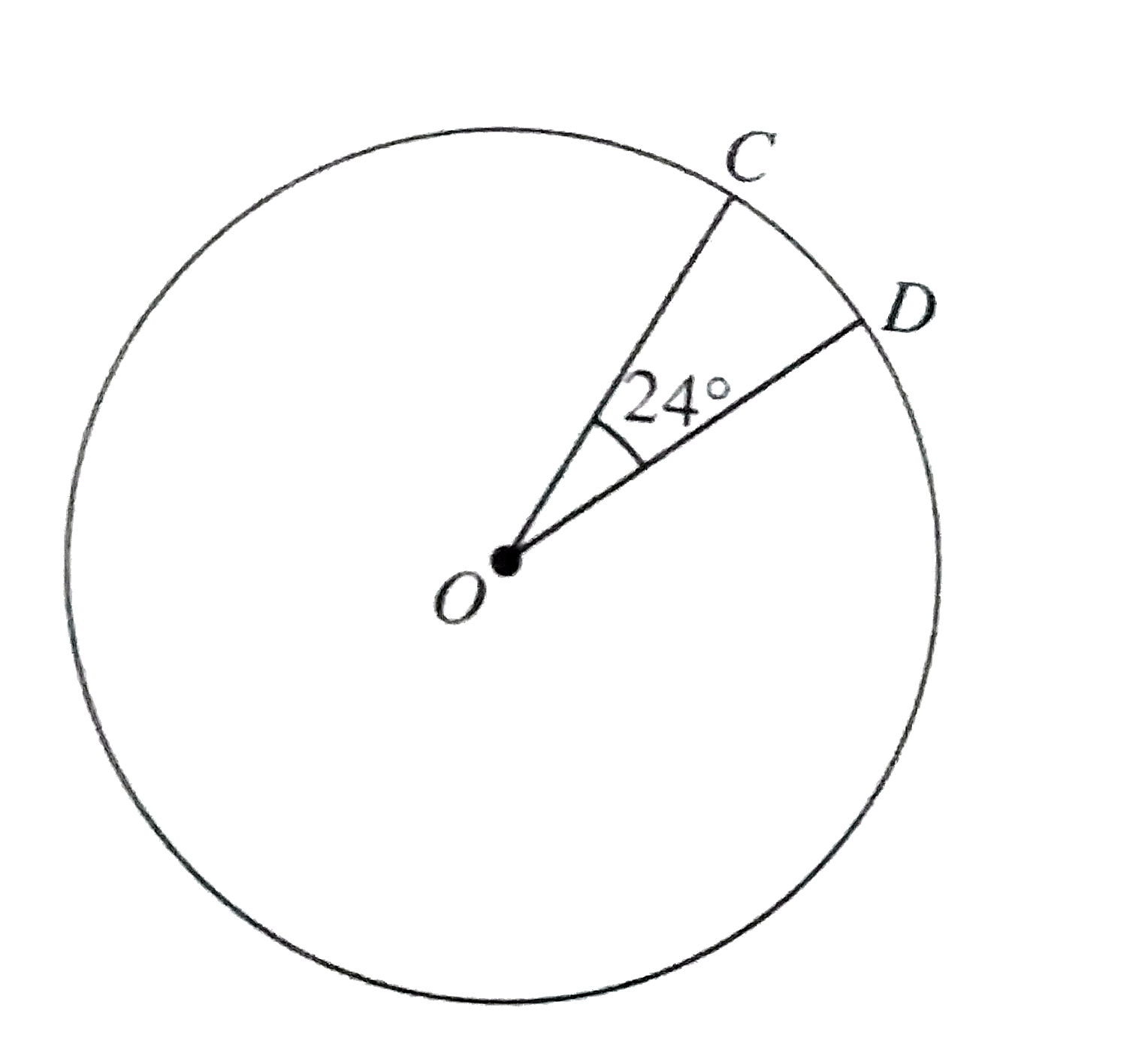 A18πB14πC1615πD83π
A18πB14πC1615πD83πIn the circle shown in the figure, the length of the arc ACB is 3 times the length of the arc AB. What is the length of the line segment AB ?
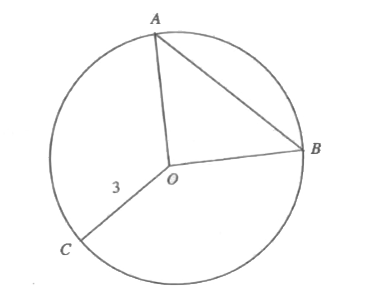 A3B4C5D3√2
A3B4C5D3√2
In the figure above, ABCD is a square with sides of 4. What is the length of arc BD?A8πB4πC2πDπ

In the figure above, AB is the are of a circle with center O. If the length of are AB is 7π, what is the area of region OAB to the nearest integer ?
View Solution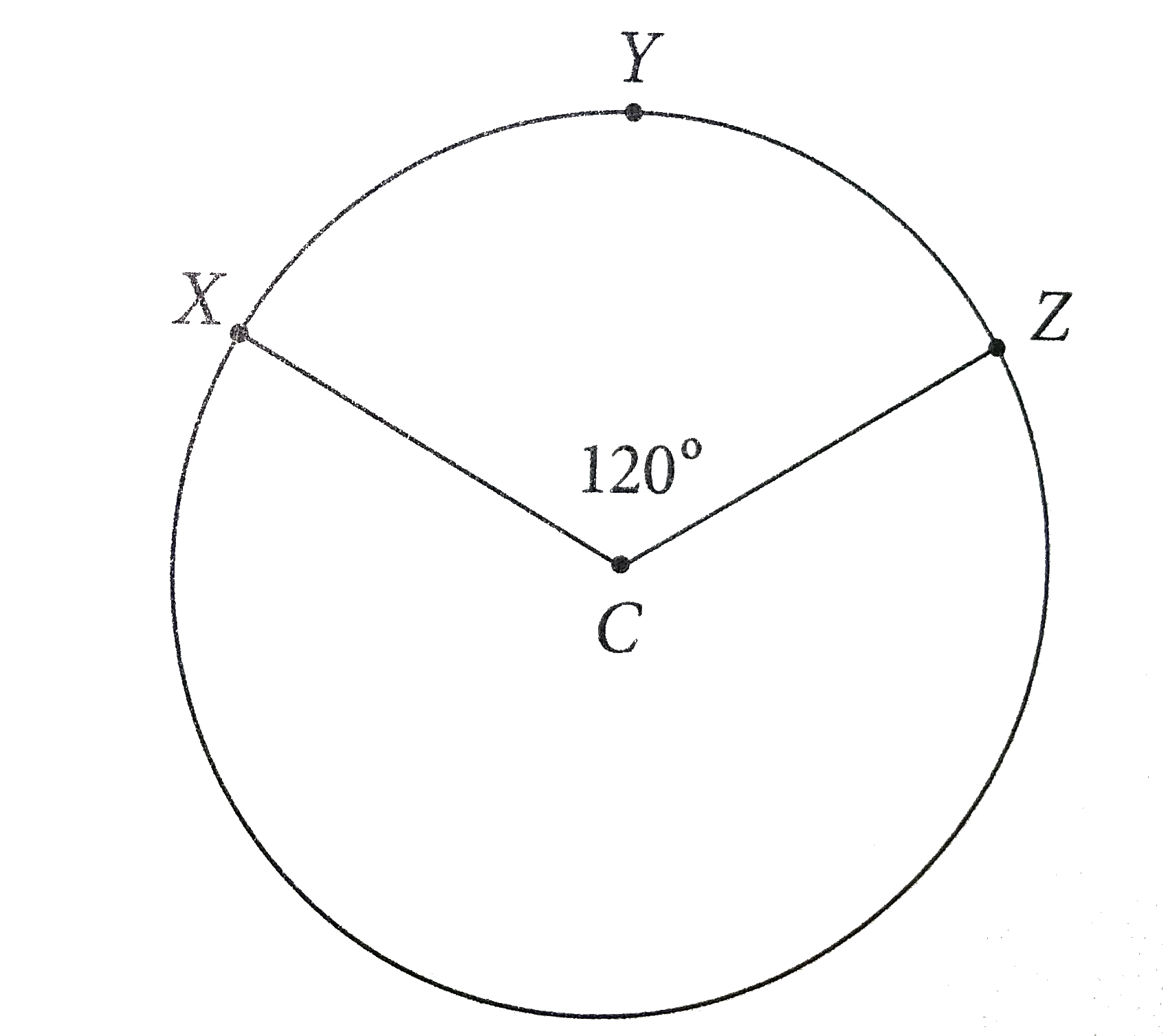
In the figure above, C is the center of a circle. If the length of the arc XYZ is 4π, what is the radius of the circle?
View Solution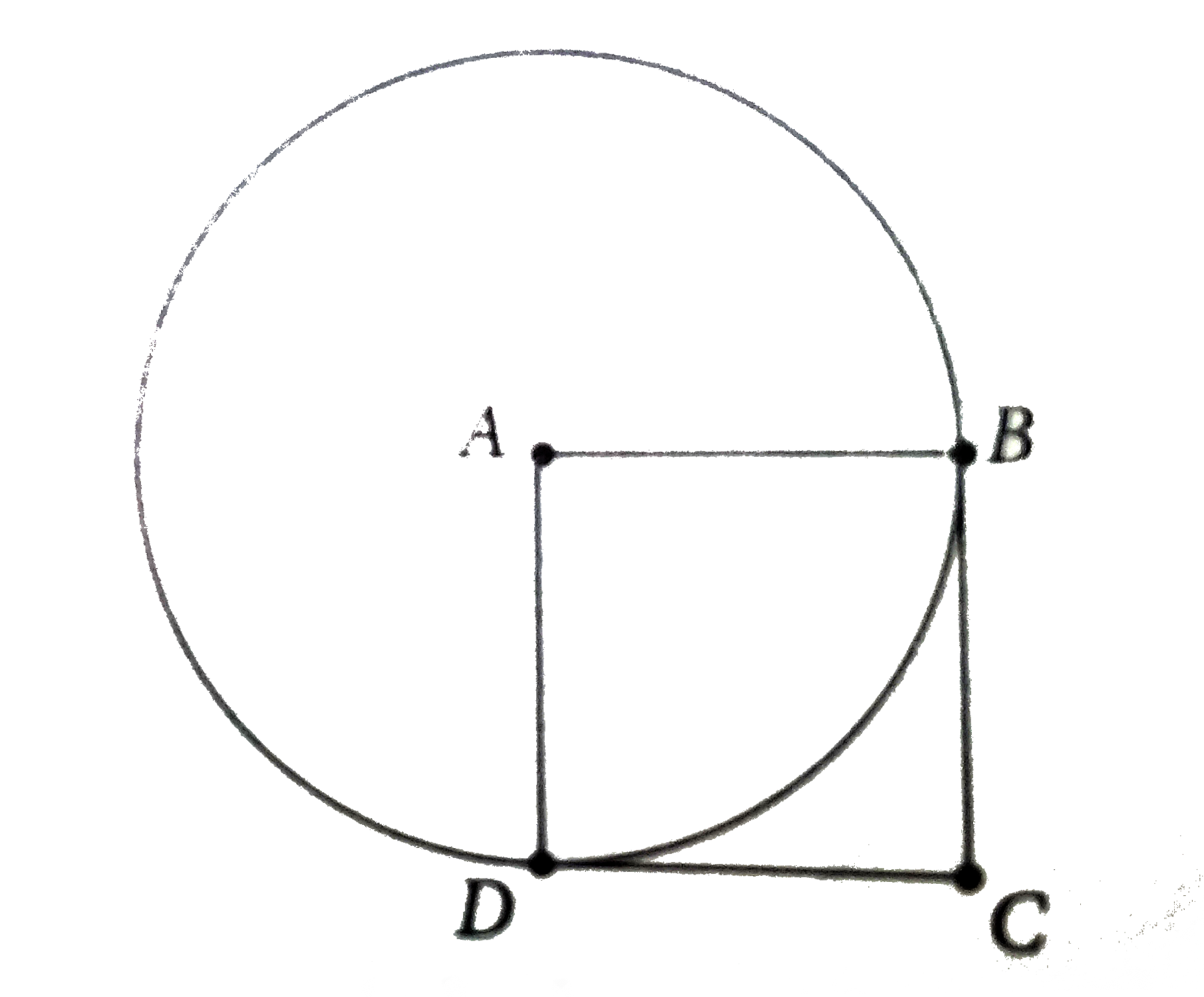
Points D and B lie on the circle above with center A. If square ABCD has an area of 16, what is the length of arc BD?
View Solution
In the diagram above, the circle has center O and diameter ¯¯¯¯¯¯AC. The measure of arc AB is 120∘ , and AO=4. What is the area of the shaded region ?
View Solution
In the xy-plane above, the circle has center O, and the measure of ∠XOY is πn radians. What is the value of n?
View Solution
