Question

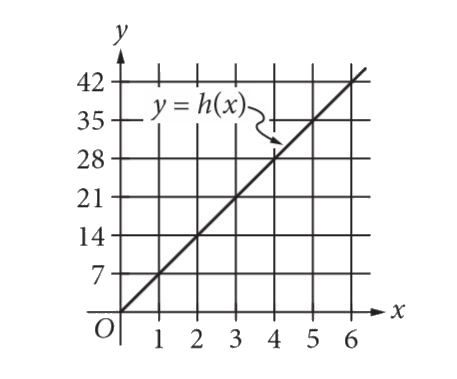
The line in the xy -plane above represents the relationship between the height h(x) , in feet, and the base diameter x , in feet, for cylindrical Doric columns in ancient Greek architecture. How much greater is the height of a Doric column that has a base diameter of 5 feet than the height of a Doric column that has a base diameter of 2 feet?

Options

A. 7 feet
B. 14 feet
C. 21 feet
D. 24 feet

Answer

C

Explanation

It’s given that the graph represents y = h(x ), thus the y-coordinate of each point on the graph corresponds to the height, in feet, of a Doric column with a base diameter of x feet. A Doric column with a base diameter of 5 feet is represented by the point (5, 35), and a Doric column with a base diameter of 2 feet is represented by the point (2, 14). Therefore, the column with a base diameter of 5 feet has a height of 35 feet, and the column with a base diameter of 2 feet has a height of 14 feet. It follows that the difference in heights of these two columns is 35 − 14, or 21 feet.
Choice A is incorrect. This value is the slope of the line and represents the increase in the height of a Doric column for each increase in the base diameter by 1 foot. Choice B is incorrect. This value represents the height of a Doric column with a base diameter of 2 feet, or the difference in height between a Doric column with base diameter of 5 feet and a Doric column with base diameter of 3 feet. Choice D is incorrect and may result from conceptual or calculation errors.