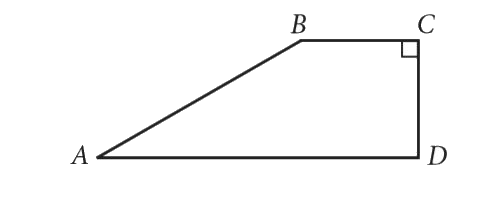
In quadrilateral ABCD above , bar(AD) bar(BC) and CD=1/2AB. What is the measure of angle B ?
In quadrilateral ABCD above , ¯¯¯¯¯¯AD¯¯¯¯¯¯BC and CD=12AB. What is the measure of angle B ?

A

150∘

B

135∘

C

120∘

D

90∘

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

A segment can be drawn inside of quadrilateral ABCD from point B to point F (not shown) on segment AD such that segment BF is perpendicular to segment AD. This will create rectangle FBCD such that FB = CD. This will also create right triangle ABF such that FB=12AB. An acute angle in a right triangle has measure 30∘ if and only if the side opposite this angle is half the length of the hypotenuse. (Such a triangle is called a 30∘−60∘−90∘ triangle), Since AB is the hypotenuse of right triangle ABF and FB=12AB, triangle ABF must be a 30∘−60∘−90∘ triangle and angle ABF must measure 60∘. The measure of angle ABC equals the sum of the measures of angles ABF and FBC. Because angle FBC is in rectangle FBCD, it has a measure of 90∘. Therefore, the measure of angle ABC, or angle B shown in the original figure, is 60∘+90∘=150∘.
Choice B is incorrect and may result from identifying triangle ABF as a 45∘−45∘−90∘ triangle and the measure of angle ABF as 45∘. Choice C is incorrect and may result from adding the measures of angles BAF and FBC rather than angles ABF and FBC. Choice D is incorrect and may result from finding the measure of angle D rather than angle B.

Updated on:21/07/2023
|