Two particles A and B of mass 1 kg and 2 kg respectively are projected in the direction shown in figure with speeds uA=200ms−1 and uB=50ms−1. Initially they were 90 m apart. Find the maximum height attained by the center of mass of the particles. Assume acceleration due to gravity to be constant. (Take, g=10ms−2.
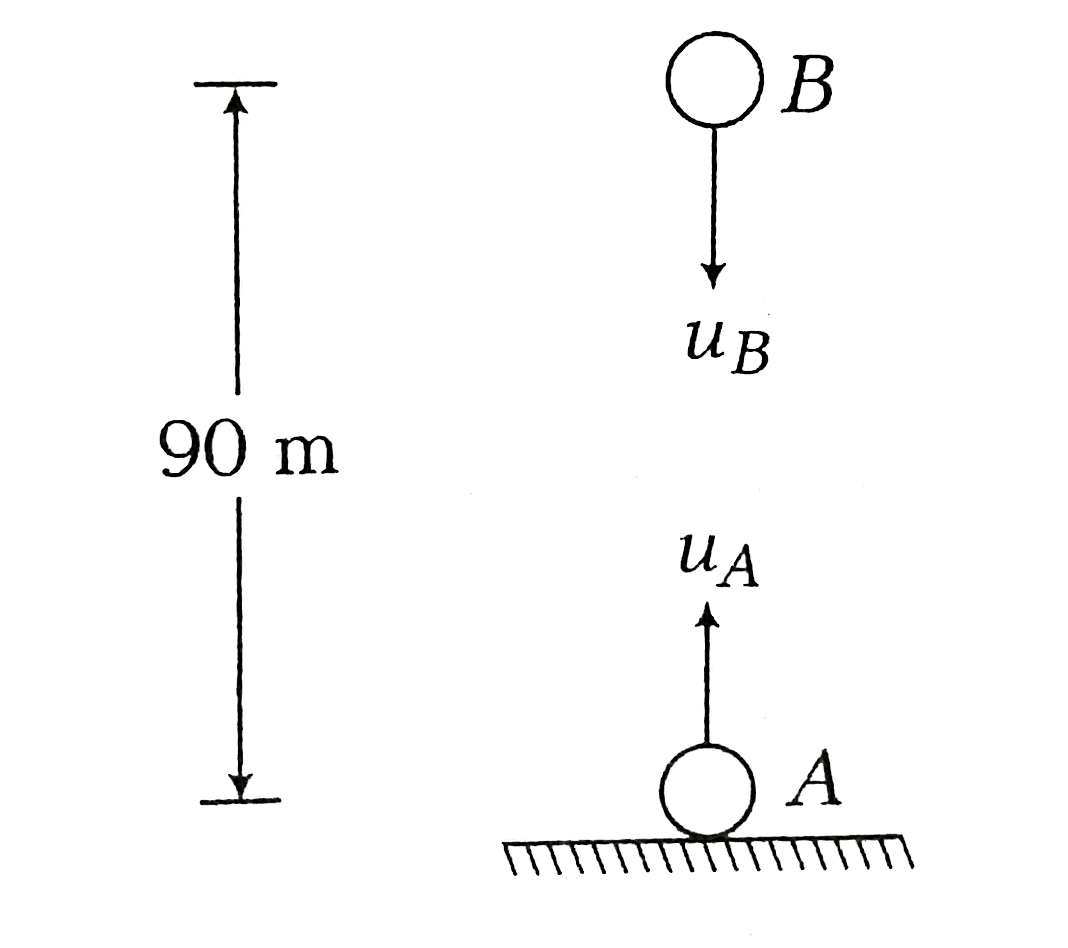
Using, mArA=mBrB or 1(rA)=2(rB)
or rA=2rB..................(i)
and rA+rB = 90 m ..........................(ii)
Solving thest two equations, we get
rA=60 m and rB =30 m
i.e., CM is at height 60 m from the ground at time t=0.
Further, aCM = mAaA+mBaBmA+mB= g = 10ms−1 (downwards)
as aA = aB) = g (downwards)
uCM = mAuA+mBuBmA+mB
1(200)−2(50)1+2=1003ms−1 (upwards)
Let h be the height attained by CM beyond 60m. Using
v2CM=v2CM+2aCMh
or 0=(1003)2−(2)(10(h)
or h=(100)2180=55.55m
Therefore, maximum height attained by the center of mass is H=60 + 55.55 = 115.55m
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Check points50videos
CENTRE OF MASS
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Taking it together73videos
CENTRE OF MASS
- BOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery38videos
CALORIMETRY AND HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
Similar Questions
Two particles A and B of masses 1kg and 2kg respectively are projected in the directions shown in figure with speeds uA=200m/s and uB=50m/s. Initially they were 90m apart. They collide in mid air and stick with each other. Find the maximum height attained by the centre of mass of the particles. Assume acceleration due to gravity to be constant.
(g=10m/s2)
 View Solution
View SolutionTwo balls A and B of equal masses are projected upward simultaneously, one from the ground with speed 50ms−1 and other from height 40m above the first ball high tower with initial speed 30ms−1. Find the maximum height attained by their centre of mass.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two particles A and B masses 1 kg and 2 kg respectivelty are projected in the same vertical line as shown in figure with speeds uA=200m/s and uB=85m/s respectively. Initially they were 90 m apart. Find the maximum height attained by the centre of mass of the system of particles A and B, from the initial position of centre of mass of the system. Assume that none of these particles collides with the ground in that duration Take g=10m/s2
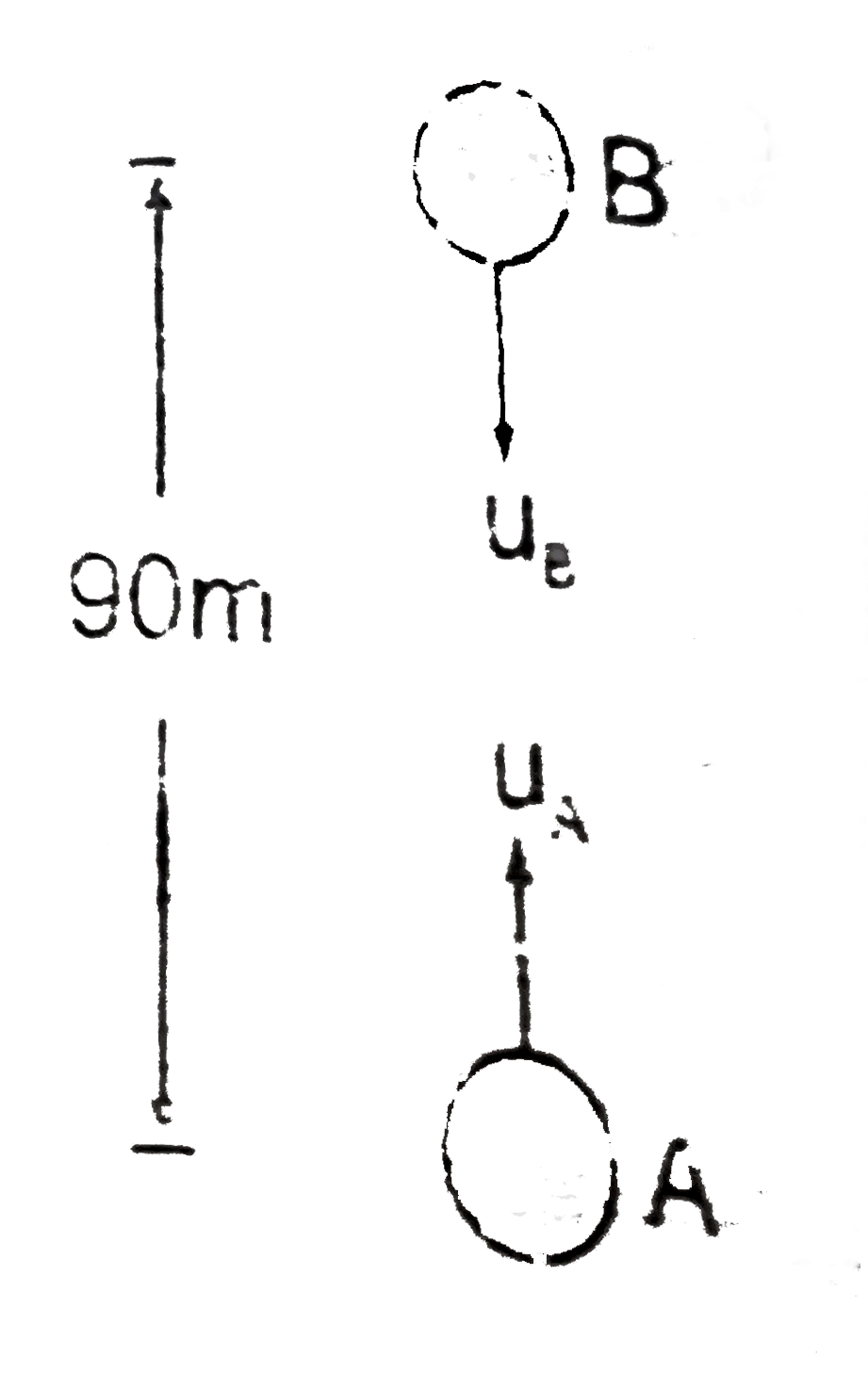 A5 meterB10 meterC25 meterD20 meter
A5 meterB10 meterC25 meterD20 meter - Question 2 - Select One
The acceleration due to gravity on a planet of mass 1025 Kg and radius 2580 Km in ms−2 is
A1B10C20D100 - Question 3 - Select One
The maximum height attained by a ball projected with speed 20ms−1 at an angle 45∘ with the horizontal is [take g = 10ms−2]
A40 mB20 mC10 mD30 m
Two particles PandQ have mass 1kgand2kg respectively. They are projected along a vertical line with velocity up=20 m/s and uQ=5 m/s when separation between them was 60 m. P was projected vertically up while Q was projected vertically down. Calculate the maximum height attained by the centre of mass of the system of two particles, measured from the initial position of P. Assume that the particles do not collide and that the ground is far below their point of projection [g=10m/s2]
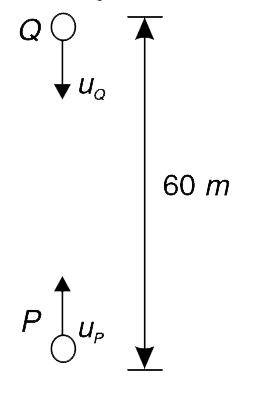 View Solution
View SolutionTwo particles of same mass are project simultaneously with same speed 20ms−1 from the top of a tower of height 30m. One is projected vertically upwards and other projected horizontally.The maximum height attained by centre of mass from the ground will be (g=10ms−2)
View SolutionTwo particles A and B of mass 3kg and 2kg moving with speed 10m/s and 5m/s as shown in figure.
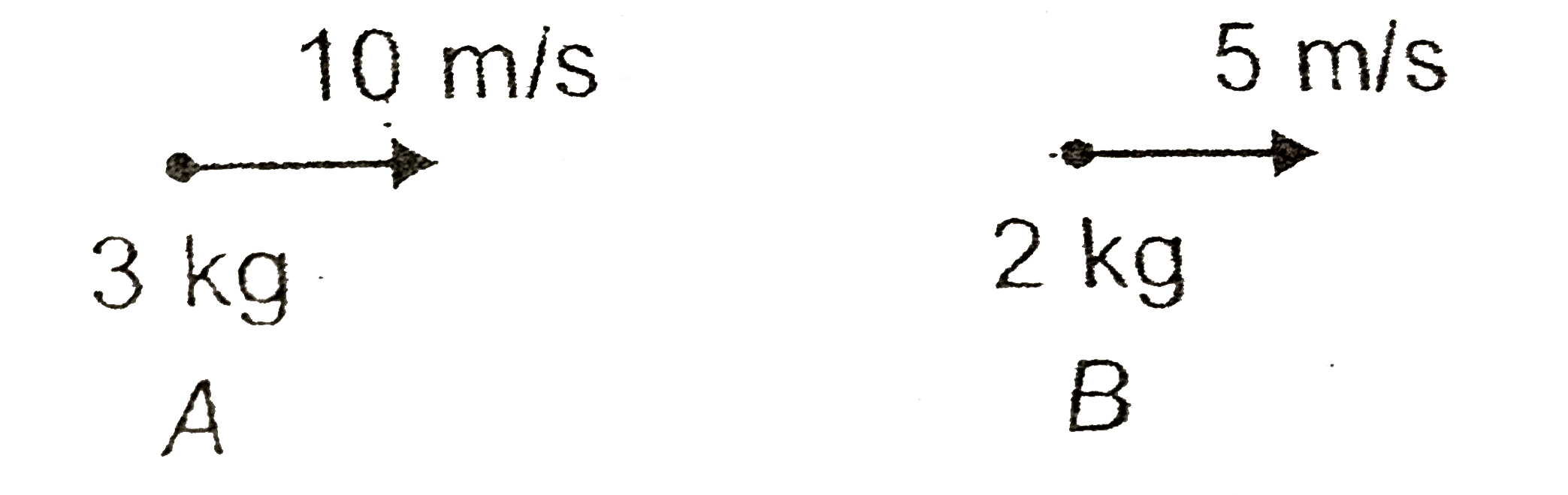
Kinetic energy of particle A when particle B has the maximum momentumView SolutionA ball is projected vertically upward with a speed of 50m/s. Find (a) the maximum height, (b) the time to reach the maximum height, (c) the speed at half the maximum height. Take g=10ms2.
View SolutionIf unit of mass is taken as 1 kg of time as 1 minute and that acceleration due to gravity is taken as 9.81ms−2 , what is the unit of energy ?
View Solution

