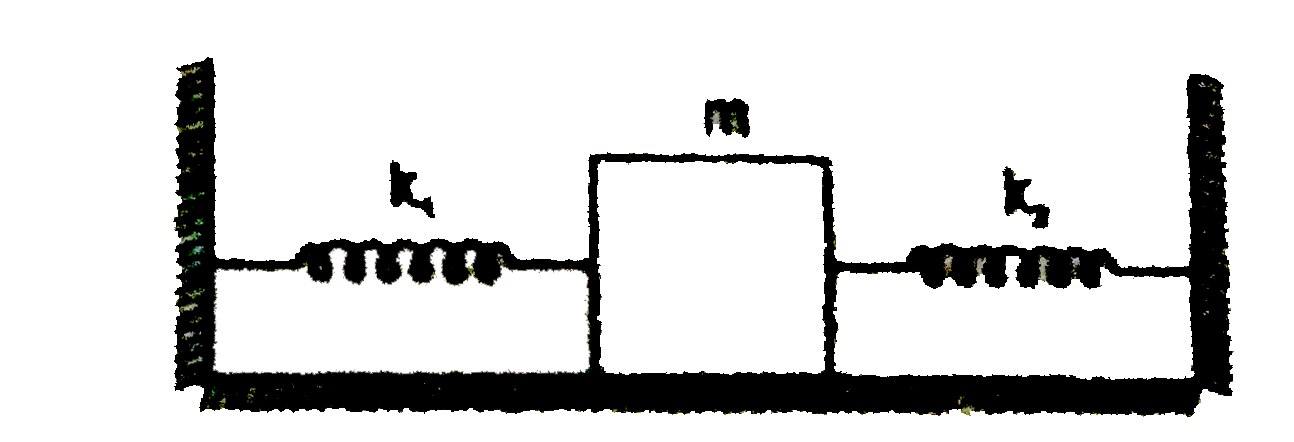
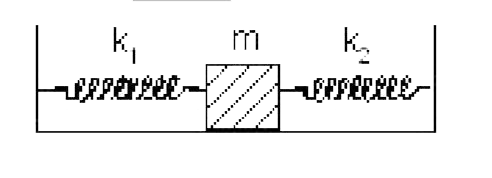
A block of mass m is attached to two unstretched springs of springs constant k1 and k2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.
k1+k2m×
k1k2m(k1+k2)×
⎷k21k22m(k1+k2)×
None of these
The correct Answer is:A
Step by step video, text & image solution for A block of mass m is attached to two unstretched springs of springs constant k_(1) and k_(2) as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - A Only One Option is Correct42videos
WORK, POWER AND ENERGY
- BOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - B More than One Option is Correct26videos
WORK, POWER AND ENERGY
- BOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY33videos
WORK, ENERGY AND POWER
Similar Questions
A block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.
 View Solution
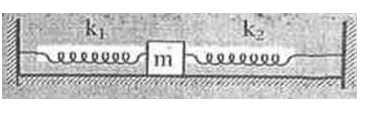
View SolutionA block of mass m is attached to two unstretched springs of spring constant k1 and k2 as shown in figure. The block is displaced towards right through a distance 'x' and is released. Find the speed of the block as it passes through a distance x/4 from its mean position. All the surfaces are smooth.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One

A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will beAx√m2kBx√2kmCxmkDx2km - Question 2 - Select One
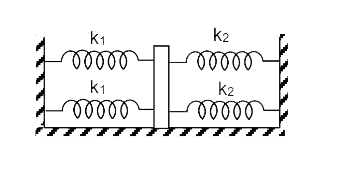
A block of mass m is attached to four unstretched massless springs of spring constant k1andk2 as shown in figure. The block is displaced towards right through distance x and is released. Speed of block when displacement of block is x/2 from mean position is :
 A√2(k1+k2)xmB√3(k1+k2)x22mC√(k1k2)3(k1+k2)mD√(k1+k2)x(k1+k2)m
A√2(k1+k2)xmB√3(k1+k2)x22mC√(k1k2)3(k1+k2)mD√(k1+k2)x(k1+k2)m - Question 3 - Select One
Two blocks (1 and 2) of equal mass m are connected by an ideal string (see figure shown) over a frictionless pulley. The blocks are attached to the ground by springs having spring constants k1 and k2 such that k1>k2
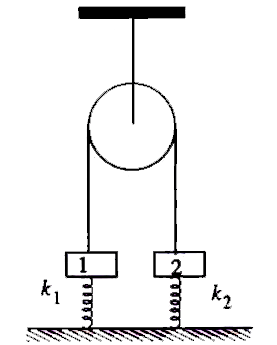
Initially, both springs are unstretched. The block 1 is slowly pulled down a distance x and released. Just after the release the possible values of the magnitude of the acceleration of the blocks a1 and a2 can be–AEither (a1=a2=(k1+k2)x2m) or (a1k1xm−ganda2=k2xm+g)B(a1=a2=(k1+k2)x2m) onlyC(a1=a2=(k1−k2)x2m) onlyD(a1=a2=(k1−k2)x2m) or (a1=a2=(k1k2)x(k1+k2)m−g)
A block of mass m = 2 kg is attached to two unstretched spring of force constant k1=100N/m and k2=125N/m
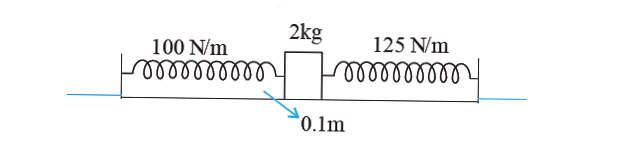
The block is displaced towards left through a distance of 10 cm and released. Find the speed of the block as it passes through the mean position.View SolutionA sping of spring constant k is attached to the ceiling. A block of mass M is attached to its lower end and is released suddenly.
(ii) Find its speed at the instant it passes throught the equilibrium position.View SolutionA block of mass m is connected between two springs (constants K1 and K2) as shown in the figure and is made to oscillate, the frequency of oscillation of the system shall be-
 View Solution
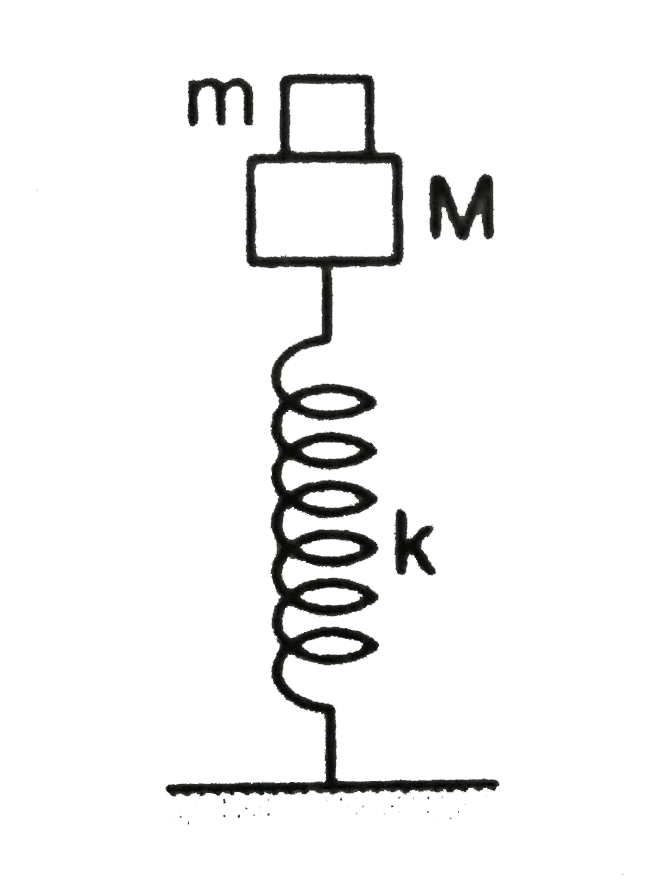
View SolutionA small block of mass m is kept on a bigger block of mass M which is attached to a vertical spring of spring constant k as shown in the figure. The system oscilates verticaly. a.Find the resultant force on the smaller block when it is displaced through a distance x above its equilibrium position. b. find the normal force on the smaller blok at this position. When is this force smallest smaller block at this position. When is this force smallest in magnitude? c. What can be the maximum amplitude with which the two blocks may oscillate together?
 View Solution
View SolutionA 2 kg block is connected with two springs of force constants k1=100N/m and k2=300N/m as shown in figure. The block is released from rest with the springs unstretched. The acceleration of the block in its lowest postion is (g=10m/s2)
 View Solution
View Solution

