Three components of a force acting on a particle are varying according to the graphs as shown. To reach at point B(8, 20, 0)m from point A(0, 5, 12)m the particle moves on paths parallel to x-axis then y-axis and then z-axis, then work done by this force is:
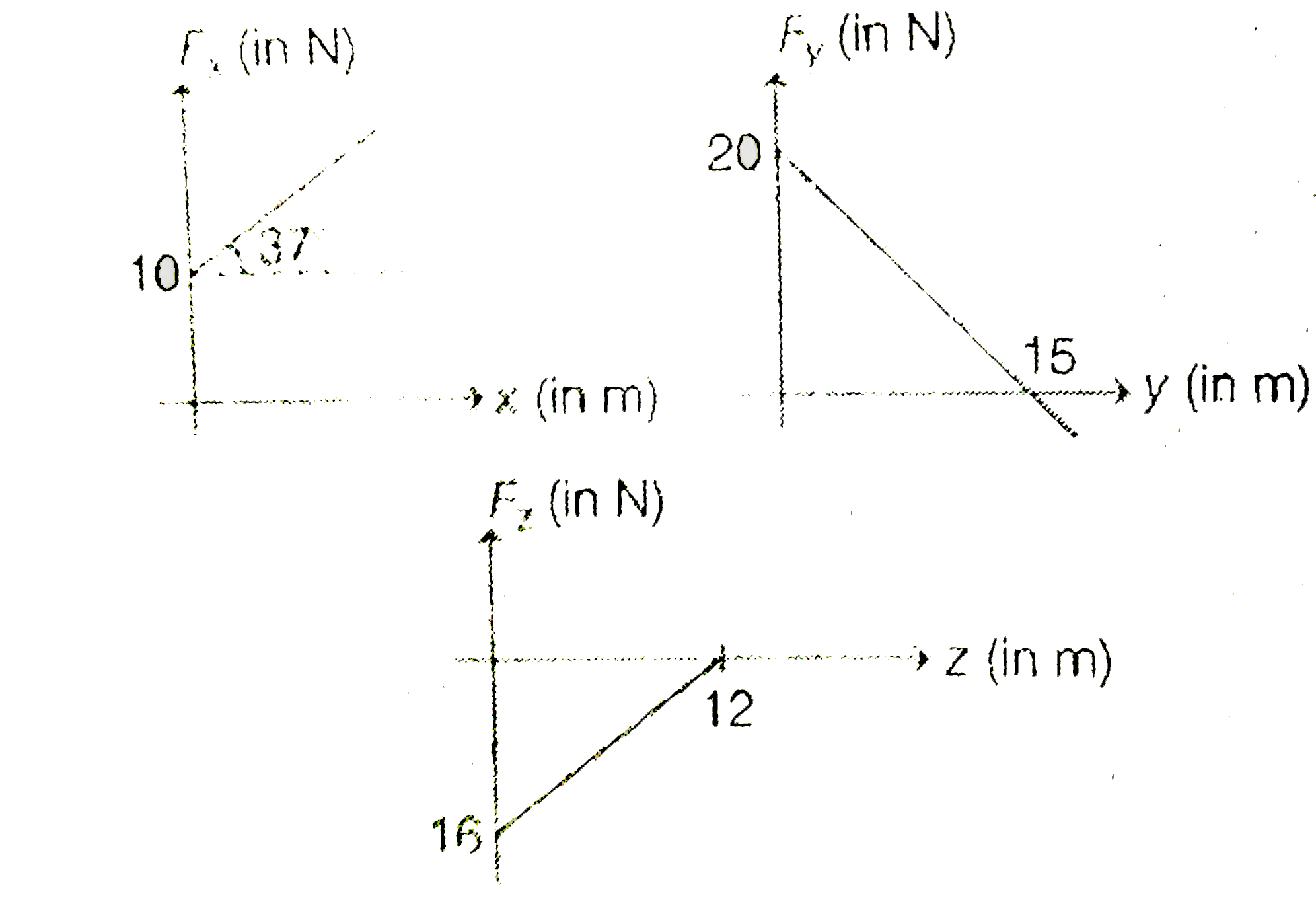
192 J
58 J
250 J
125 J
The correct Answer is:C
Step by step video, text & image solution for Three components of a force acting on a particle are varying according to the graphs as shown. To reach at point B(8, 20, 0)m from point A(0, 5, 12)m the particle moves on paths parallel to x-axis then y-axis and then z-axis, then work done by this force is: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - B More than One Option is Correct26videos
WORK, POWER AND ENERGY
- BOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - C Comprehension Type Questions18videos
WORK, POWER AND ENERGY
- BOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions11videos
WORK, POWER AND ENERGY
- BOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY33videos
WORK, ENERGY AND POWER
Similar Questions
. Knowledge Check
- Question 1 - Select One
The force F acting on a particle is moving in a straight line as shown in figure. What is the work done by the force on the particle in the 4 m of the trajectory?
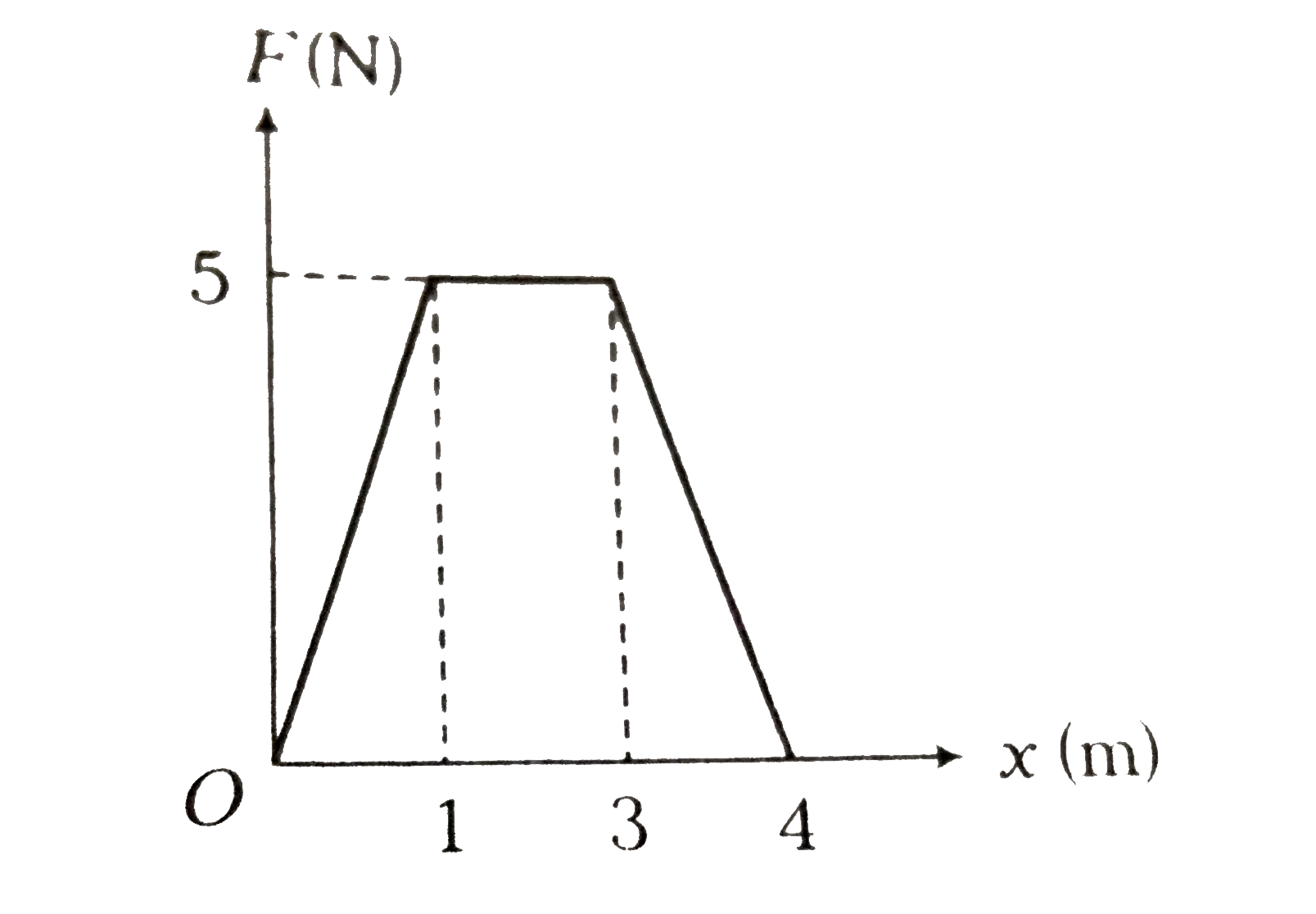A5 JB10 JC15 JD2.5 J - Question 2 - Select One
A force F=−K(yˆi+xˆj), acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0) and then parallel to the y-axis to the point (a, a). The total work done by the force is
A−2Ka2B2Ka2C−Ka2DKa2 - Question 3 - Select One
A force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
A−2Ka2B2Ka2C−Ka2DKa2
A force →F=(4ˆi+5ˆj)N acts on a particle moving in XY plane. Starting from origin, the particle first goes along x-axis to the point (5.0) m and then parallel to the Y-axis to the point (5,4 m. The total work done by the force on the particle is
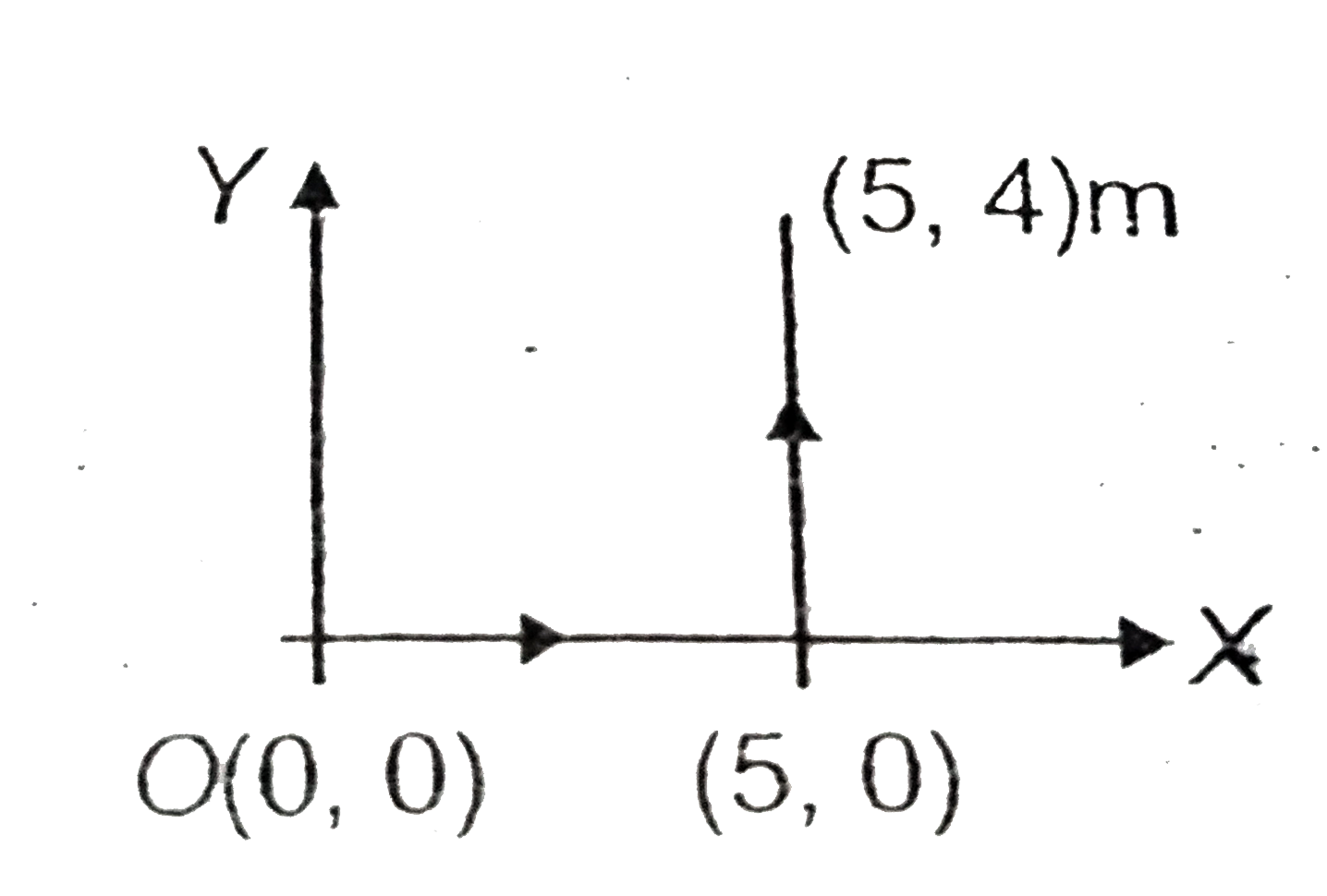View SolutionForce acting on a particle varies with x as shown in figure. Calculate the work done by the force as the particle moves from x = 0 to x = 6.0 m.
View SolutionA force F=−k(^ˆi+xˆj) (where k is a positive constant) acts on a particle moving in the x−y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0) and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
(a) −2ka2 , (b) 2ka2,(c)-ka^(2),(d)ka^(2)View SolutionA force →F(yˆl+xˆJ), where K is a positive constant, acts on a particle moving in the XY-Plane. Starting from the origin, the particle is taken along the positive X-axis to a point (a,0) and then parallel to the y-axis to the point (a,a). Calculate the total work done by the force on the particle.
View SolutionA force F acting on a particle varies with the position x as shown in the graph. Find the work done by the force in displacing the particle from x=−a to x=+2a.
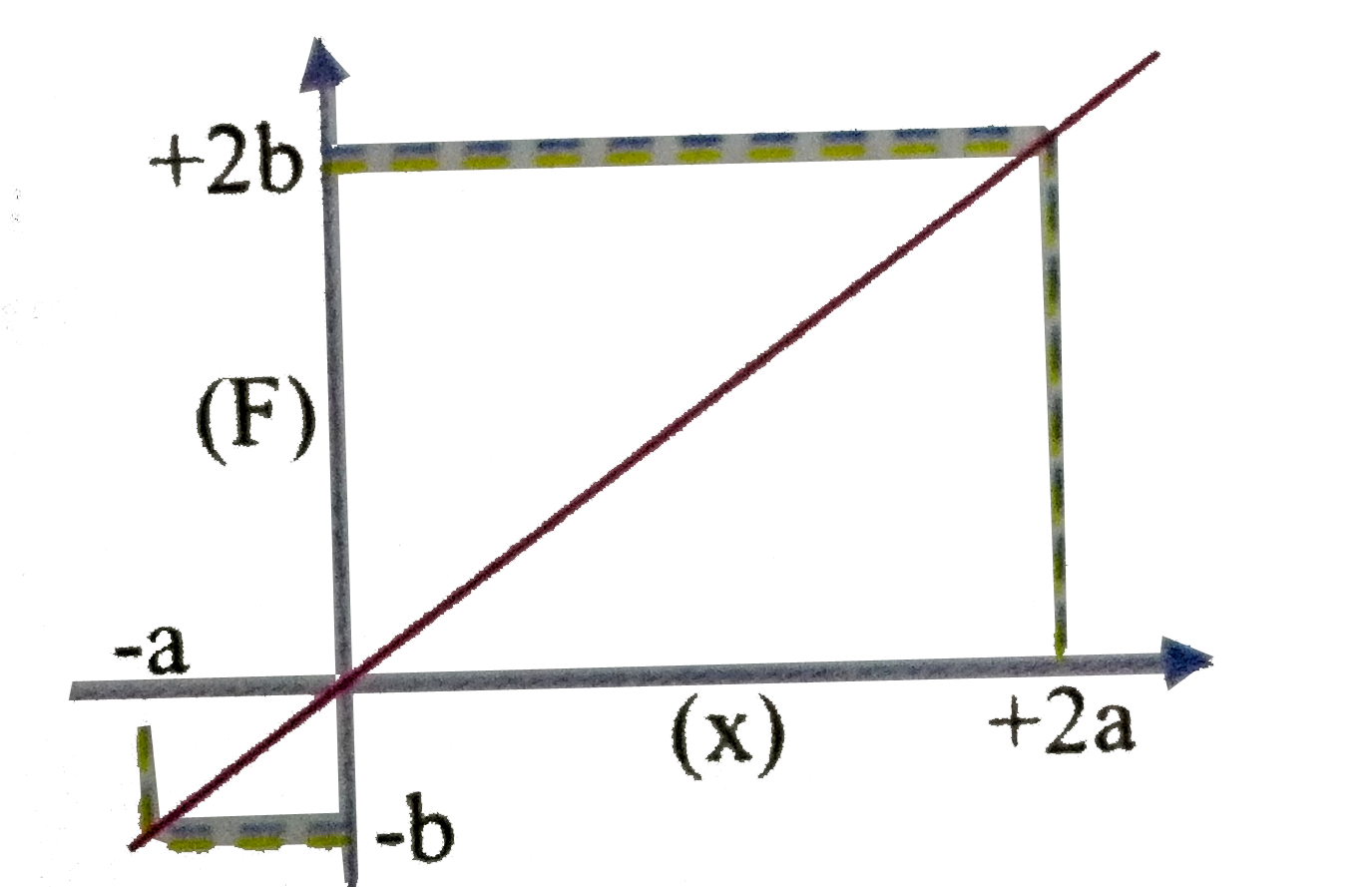.View Solution
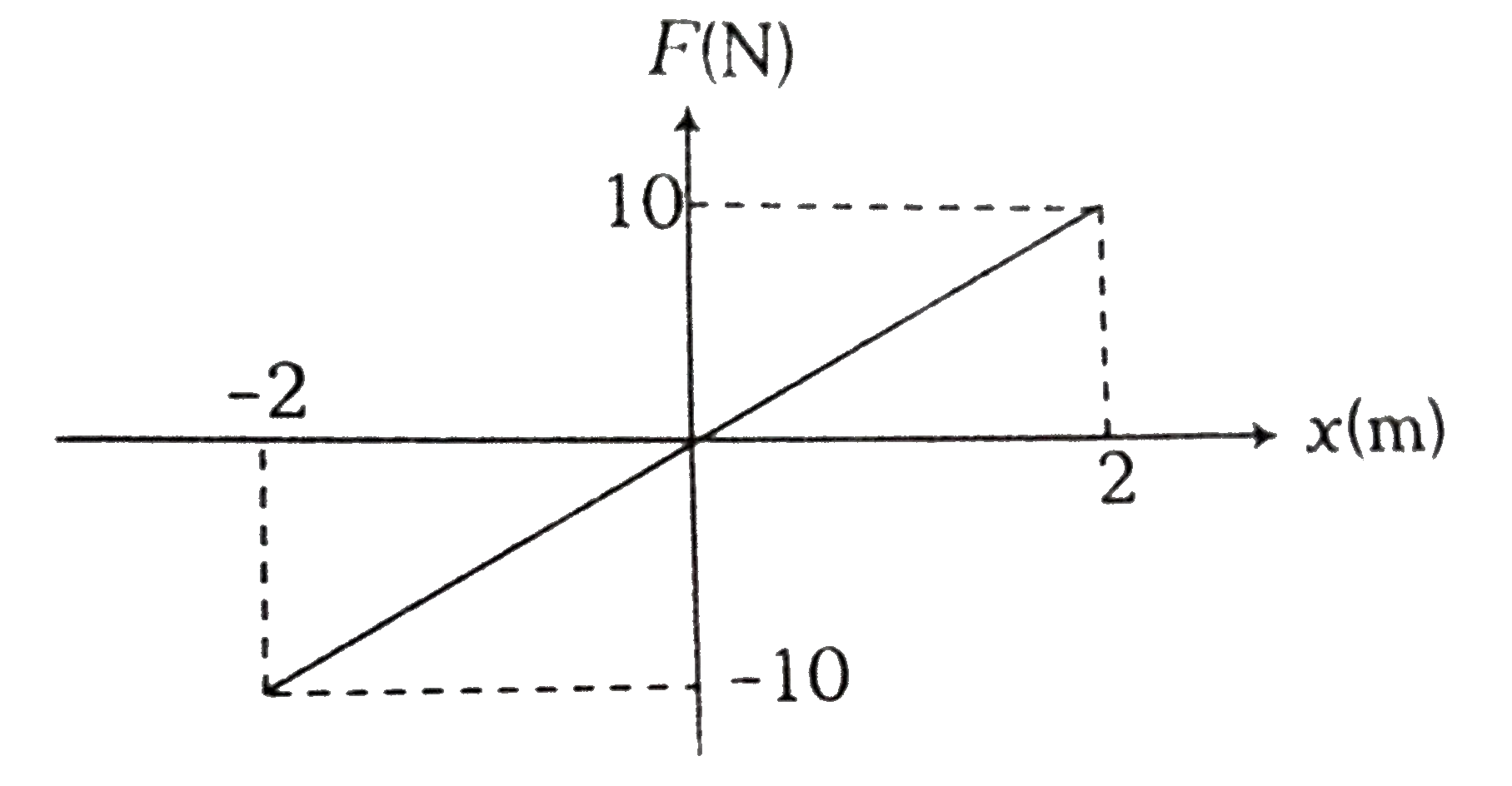