The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity v0 as shown. The length of the rod is l. At the instant when θ=37∘
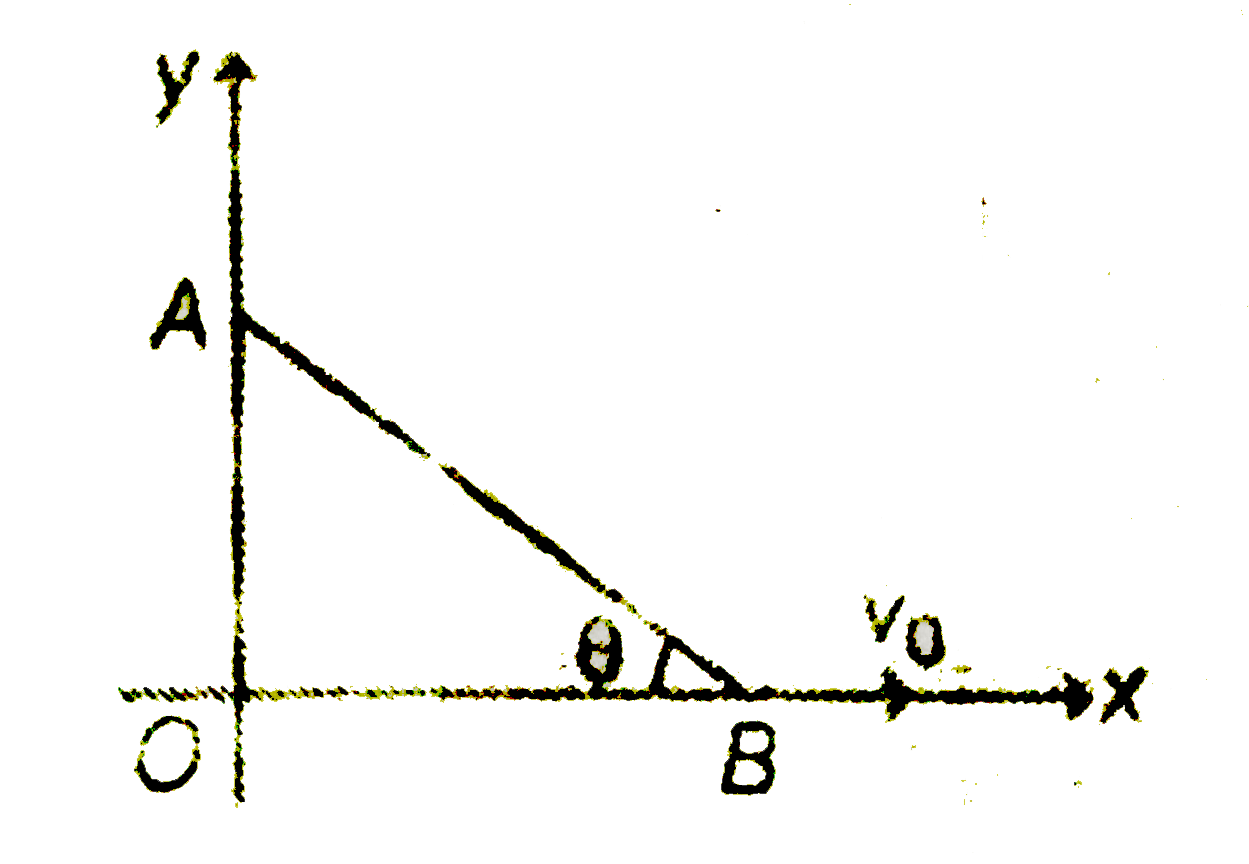
velocity of end A is 43v0 downwards
angular velocity of rod is 53v0l
angular velocity of rod is constant
velocity of end A is constant
The correct Answer is:A, B, D
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
41 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Matrix Matching Type Questions
17 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - A Only One Option is Correct
86 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
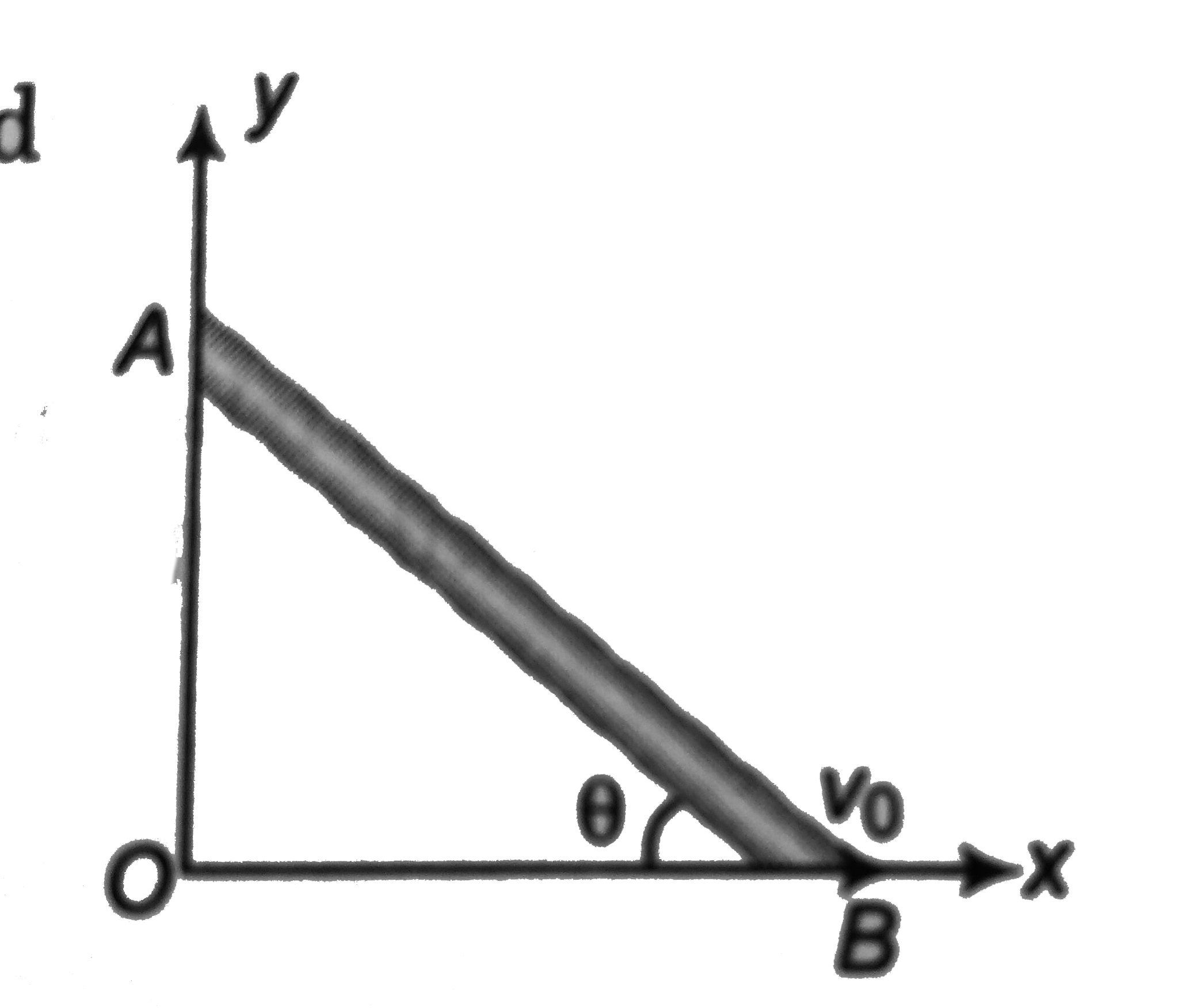
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity vv as shown. The length of the rod is l.
View SolutionThe end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity v0 as shown. The length of the rod is l. At the instant when θ=37∘, the angular velocity of the rod is pqv0l. Find (p+q).
'(##CEN_KSR_PHY_JEE_C07_009_Q05##) '
View Solution
Knowledge Check

The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity vv as shown. The length of the rod is l.AAt θ=37∘ velocity of end A is 43v0 downwardsBAt θ=37∘ angular velocity of rod is 5v03lCAngular velocity of rod is constantDvelocity of end A is constant.End A of a rod AB is being pulled on the floor with a constant velocity v0 as shown. Taking the length of the rod as l, at an instant when the rod makes an angle 37∘ with the horizontal, calculate

the velocity of the CM of the rodA57v0 at tan−143 below horizontalB57v0 at tan−134 below horizontalC56v0 at tan−134 below horizontalD56v0 at tan−143 below horizontal
A rod of length 'l' is inclined at an angle 'θ' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1, what is the velocity of end B at the instant when rod makes 'θ' angle with the horizontal.
View SolutionA rod of length 'l' is inclined at an angle 'theta' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1 what is the velocity of end B at the instant when rod makes 'theta' angle with the horizontal .
View SolutionA rod of length 'l' is inclined at an angle 'θ' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1, what is the velocity of end B at the instant when rod makes 'θ' angle with the horizontal.
View SolutionA conducting rod AB of lemgth 2 l moves through a uniform magnetic field B. The rod makes an angle θ with the vertical while it falls with a uniform linear velocity v. The potential difference between the two ends of the rod is Bv2l .

View SolutionA conducting rod AB of lemgth 2 l moves through a uniform magnetic field B. The rod makes an angle θ with the vertical while it falls with a uniform linear velocity v. The potential difference between the two ends of the rod is Bv2l .

View SolutionFigure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity v. Find the velocity of the other end B downward when the rod makes an angle θ with the horizontal.

View Solution
