An L shaped frame is free to rotate in a vertical plane about a horizontal axis passing through a smooth hinge O. Each side of the frame has a length L and mass m. Frame is let to fall with one side horizontal and the other vertical.
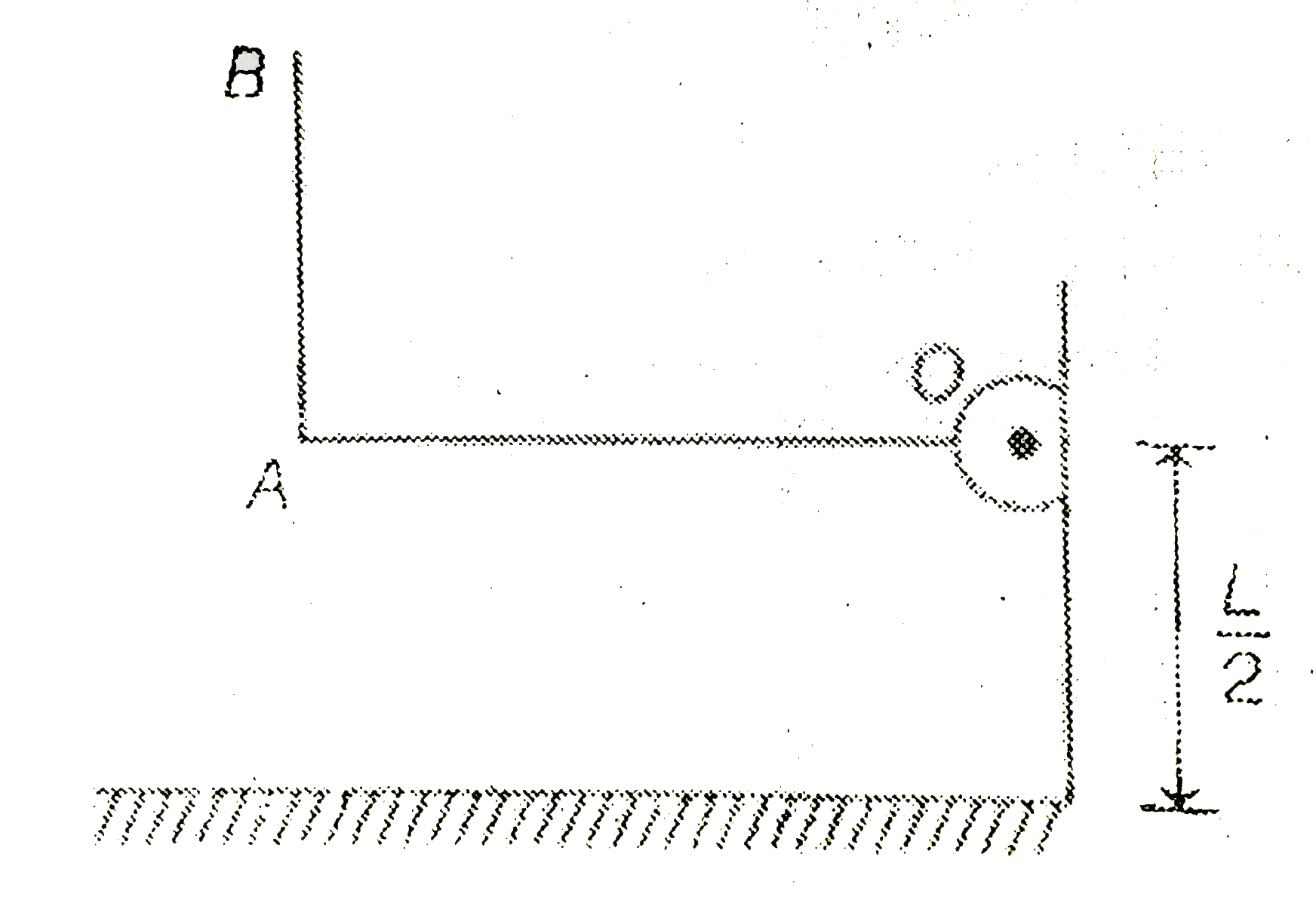
Angular acceleration of the frame just after it is allowed to fall is
4g3L
9g10L
g2L
3g2L
The correct Answer is:B
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Matrix Matching Type Questions
17 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
An L shaped frame is free to rotate in a vertical plane about a horizontal axis passing through a smooth hinge O. Each side of the frame has a length L and mass m. Frame is let to fall with one side horizontal and the other vertical.

With what speed the end A will strike the ground ?
View SolutionA L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is

View Solution
Knowledge Check
An L shaped frame is free to rotate in a vertical plane about a horizontal axis passing through a smooth hinge O. Each side of the frame has a length L and mass m. Frame is let to fall with one side horizontal and the other vertical.

With what speed the end A will strike the ground ?A√gLB2√gLC3.2√gLD1.6√gLA massless stick of length L is hinged at one end and a mass m attached to its other end. The stick is free to rotate in vertical plane about a fixed horizontal axis passing through frictionless hinge. The stick is held in a horizontal position. At what distance x from the hinge should a second mass M = m be attached to the stick, so that stick falls as fast as possible when released from rest
 A√2LB√3LC(√2−1)LD(√3−1)L
A√2LB√3LC(√2−1)LD(√3−1)LThree massless rods are fixed to form a right angled triangular frame such that AB=BC=1 . Two identical small objects of mass m are fixed at A and C . The frame is hinged about B such that the frame can rotate in vertical plane about an horizontal axis without friction. Initially AB is vertical and BC is horizontal and the system is released from rest.
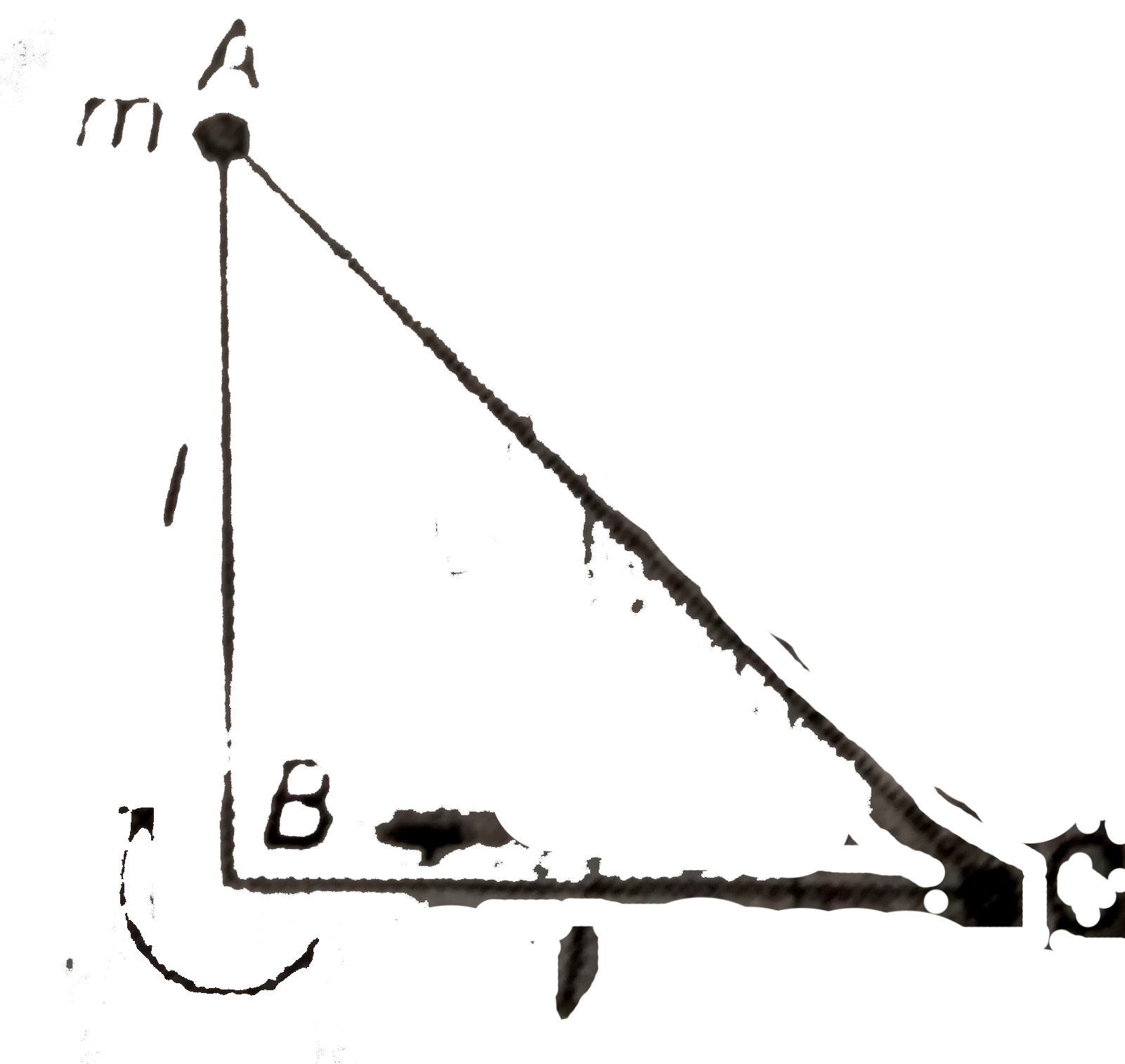
The magnitude of acceleration of mass A when the rod AC becomes horizontal isAg(1+√2)Bg(2+√2)C2g(1+√2)Dg(√2−1)
A L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is

View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View SolutionThree massless rods are fixed to form a right angled triangular frame such that AB=BC=1 . Two identical small objects of mass m are fixed at A and C . The frame is hinged about B such that the frame can rotate in vertical plane about an horizontal axis without friction. Initially AB is vertical and BC is horizontal and the system is released from rest.

The magnitude of acceleration of mass A when the rod AC becomes horizontal is
View SolutionA long uniform rod of length L, mass M is free to rotate in a horizontal plane about a vertical axis through its end. Two springs of constant K each are connected as shown. On equilibrium, the rod was horizontal. The frequency will be –
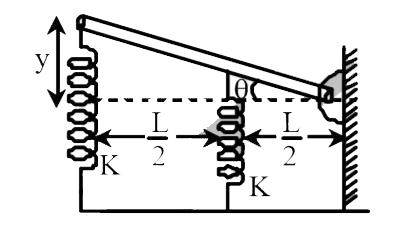
View SolutionA wire frame AOPQB, lying in the horizontal plane, is free to rotate about a vertical axis passing through center C of the same circle and ⊥ to plan of AOPQB. The mass M of the frame is uniformly distributed over its whole length. The moment of inertia of the frame about this axis, is ( OA=QB-r and CP =r the ratio of semicircular part)
View Solution
