A wheel of radius R=2m performs pure rolling on a rough horizontal surface with speed v=10 m/s . In the figure shown, angle θ is angular position of point P on wheel reaches the maximum height from ground. Find the value of secθ (take g=10m/s2).
The correct Answer is:5
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Matrix Matching Type Questions
17 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A wheel of radius R=0.1m is rolling without slipping on a horizontal surface as shown in the firgure. Centre of the wheel moves with a constant speed √3m/s. The speed of the point P with respect to ground is
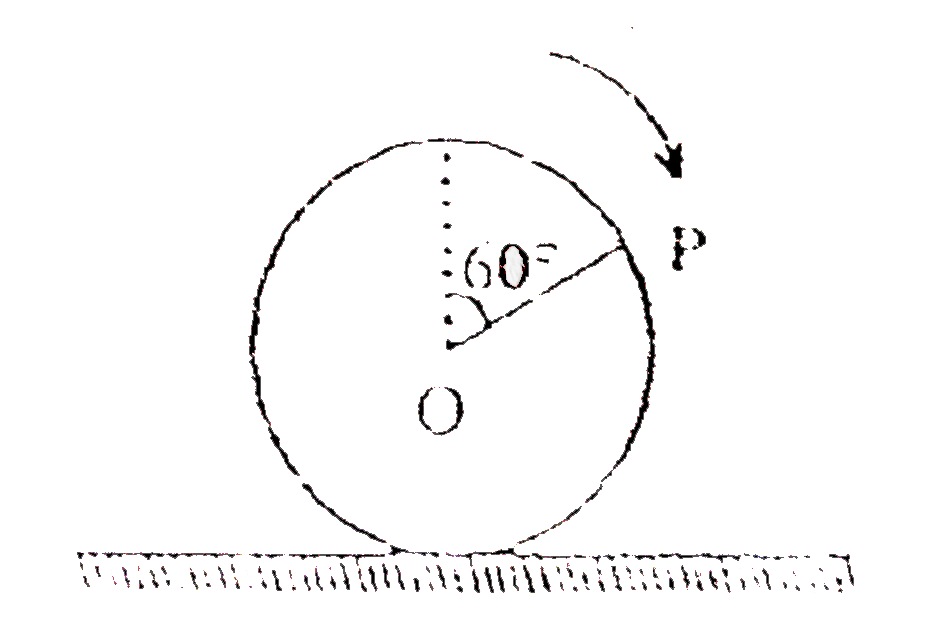
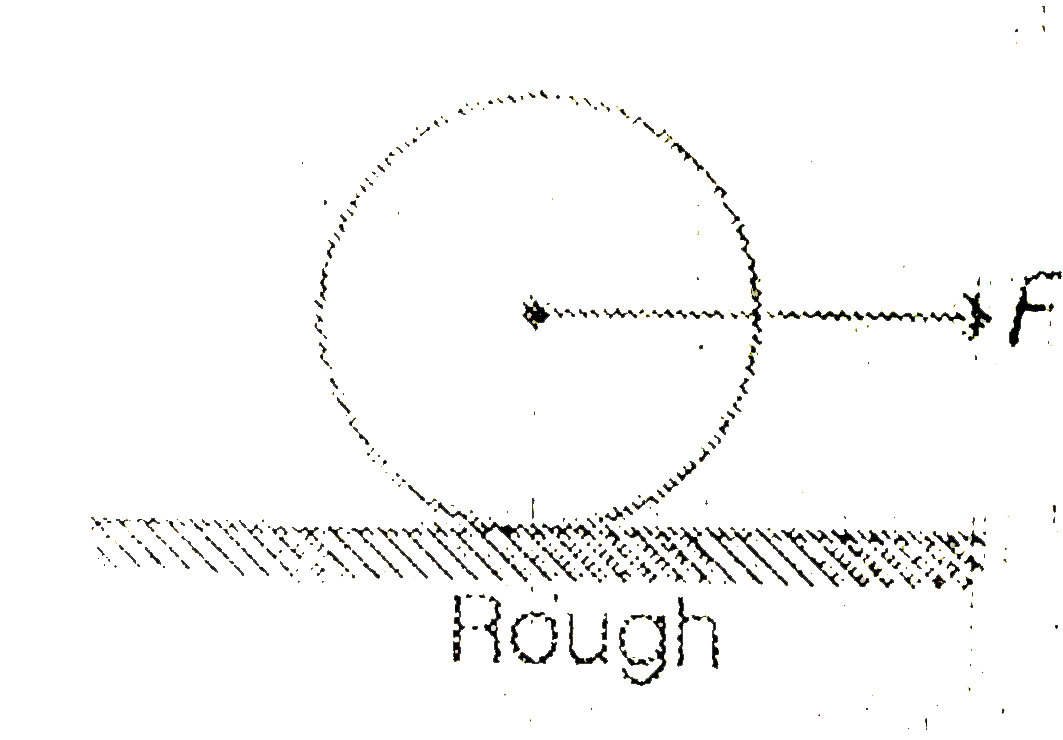
View SolutionA solid cylinder of mass M and radius R pure rolls on a rough surface as shown in the figure. Choose the correct alternative (s).
View Solution
Knowledge Check
A wheel of radius R=0.1m is rolling without slipping on a horizontal surface as shown in the firgure. Centre of the wheel moves with a constant speed √3m/s. The speed of the point P with respect to ground is
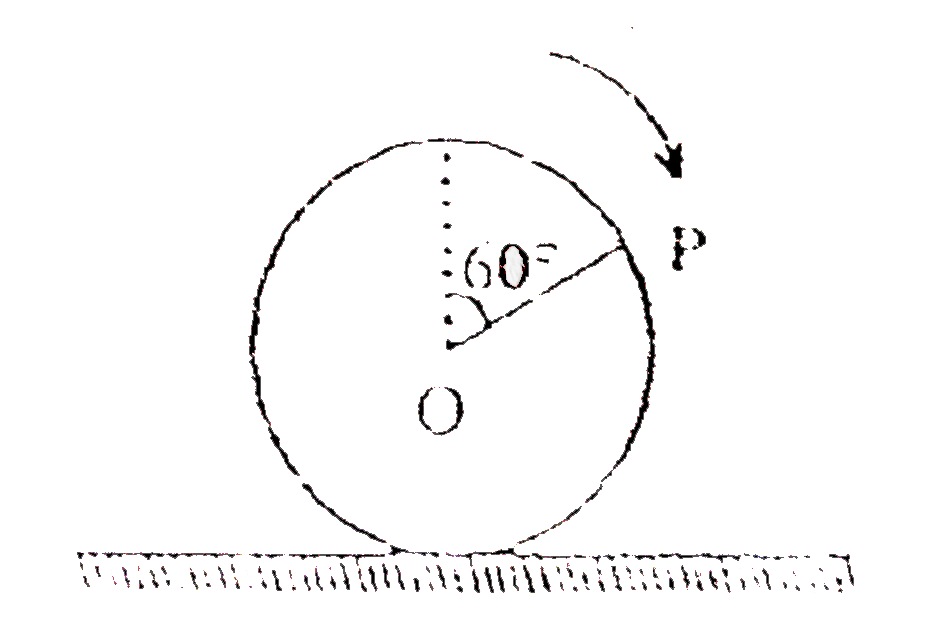 A2√3m/sBzeroC3 m/sD√3m/s
A2√3m/sBzeroC3 m/sD√3m/sA solid cylinder of mass M and radius R pure rolls on a rough surface as shown in the figure. Choose the correct alternative (s).
 AThe acceleration of the centre of mass is FMBThe acceleration of the centre of mass is 23FMCThe friction force on the cylinder acts backwardDThe magnitude of the friction force is F3
AThe acceleration of the centre of mass is FMBThe acceleration of the centre of mass is 23FMCThe friction force on the cylinder acts backwardDThe magnitude of the friction force is F3The wheel of radius R rolls with out slipping on horizontal rough surface, and its centre O has an horizontal acceleration in a0 forward direction. A point P on the wheel is a distancer r from O and angular position θ from horizontal. For the given values of a0 R and r, determine the angle θ for which point P has no acceleration in this position.
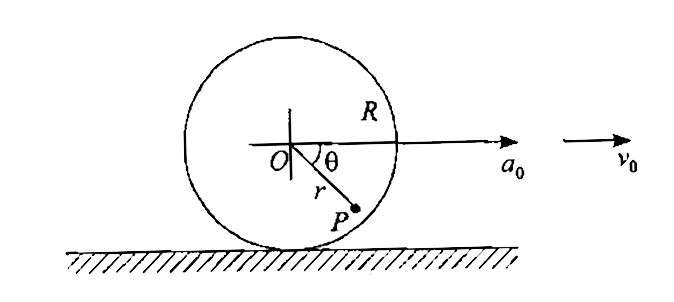 Acos1.rRBtan1.rRCsin1.rRDcos1.r2R
Acos1.rRBtan1.rRCsin1.rRDcos1.r2R
A disc shaped body (having a hole shown in the figure) of mass m=10kg and radius R=109m is performing pure rolling motion on a rough horizontal surface. In the figure point O is geometrical center of the disc and at this instant the centre of mass C of the disc is at same horizontal level with O. The radius of gyration of the disc about an axis pasing through C and perpendicular to the plane of the disc is R2 and at the insant shown the angular velocity of the disc is ω=√gR rad/sec in clockwise sence. g is gravitation acceleration =10m/s2. Find angular acceleation α ( in rad/s2) of the disc at this instant.

View SolutionA disc shaped body (having a hole shown in the figure) of mass m=10kg and radius R=109m is performing pure rolling motion on a rough horizontal surface. In the figure point O is geometrical center of the disc and at this instant the centre of mass C of the disc is at same horizontal level with O. The radius of gyration of the disc about an axis pasing through C and perpendicular to the plane of the disc is R2 and at the insant shown the angular velocity of the disc is ω=√gR rad/sec in clockwise sence. g is gravitation acceleration =10m/s2. Find angular acceleation α ( in rad/s2) of the disc at this instant.

View SolutionA ball is thrown at a speed of 40 m/s at an angle of 600 with the horizontal. Find a. the maximum height reached and b. the range of te ball. Take g=10ms2.
View SolutionA ball is thrown at a speed of 40 m/s at an angle of 600 with the horizontal. Find a. the maximum height reached and b. the range of te ball. Take g=10ms2.
View SolutionThe wheel of radius R rolls without slipping on horizontal rough surface, and its centre O has an horizontal acceleration a0 in forward direction. A point P on the wheel is a distance r from O and angular position θ from horizontal. For a given values of a0, R and r, determine the angle θ for which point P has no acceleration in this position.
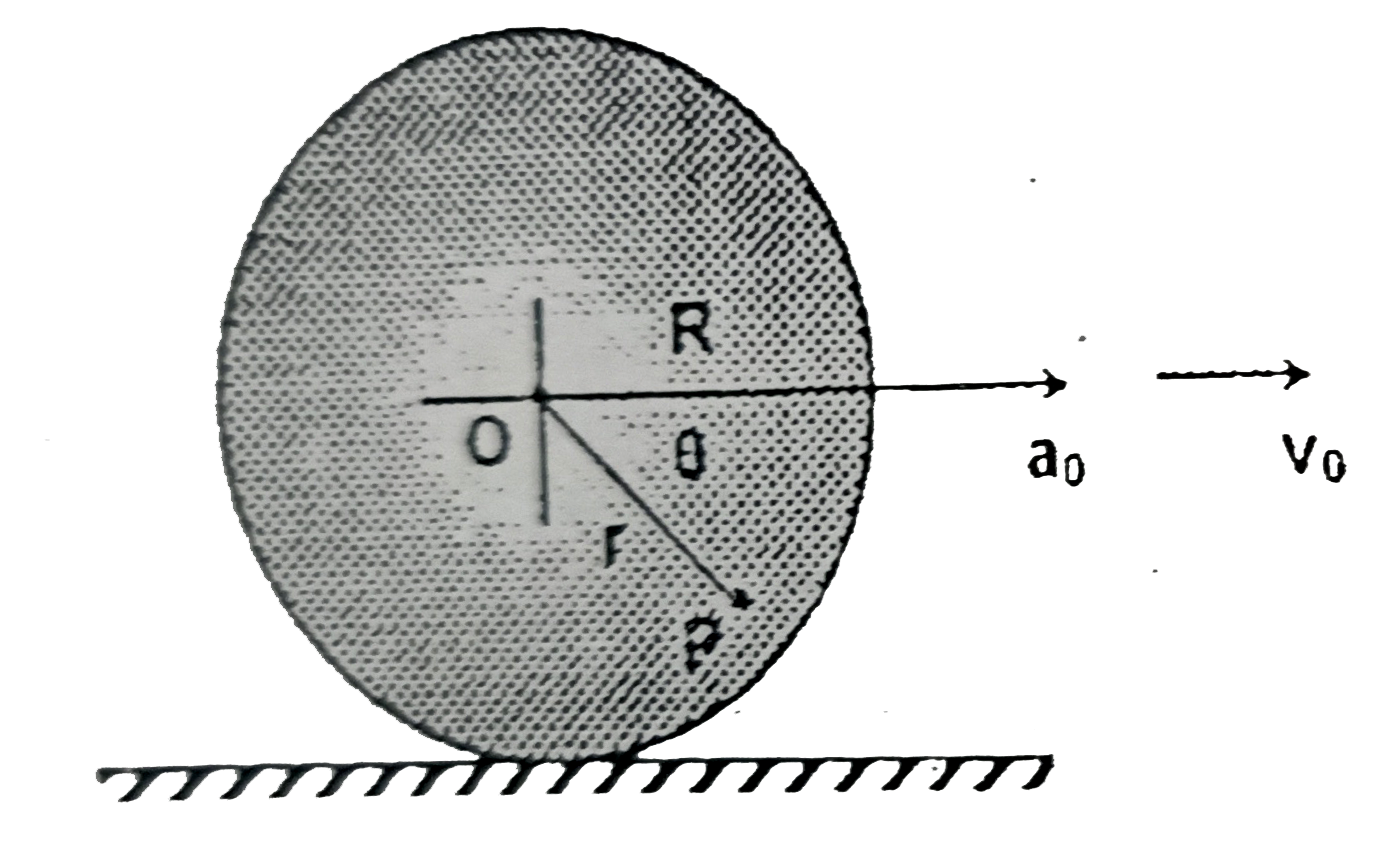
View Solution
