In order to produce a longitudinal strain of 2×10−4, a stress of 2.4×107Nm−2 is produced in a wire. Calculate the Young's modulus of the material of the wire.
The correct Answer is:1.2×101!Nm−2
Step by step video, text & image solution for In order to produce a longitudinal strain of 2xx10^(-4), a stress of 2.4xx10^(7) Nm^(-2) is produced in a wire. Calculate the Young's modulus of the material of the wire. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
The length of a suspended loire increases by 10−4 of its original length when a stress of 107Nm−2 is applied on it. Calculate the Young's modulus of the material of the wire.
View SolutionA wire increases by 10−3 of its length when a stress of 1×108Nm−2 is applied to it. What is the Young's modulus of the material of the wire?
View Solution
Knowledge Check
- Question 1 - Select One
If stress is 1012 times the strain produced in a wire, then its Young's modulus will be
A1012 unitsB10−12 unitsC1024 unitsD10−24 units - Question 2 - Select One
If x is the strain produced in a wire having the Young's modulus Y, then the strain energy per unit volume is
A12YxBYx2C12Yx2Dx2Y - Question 3 - Select One
When a wire is stretched by a force the strain produced in the wire is 2×10−4. If the energy stored per unit volume of the wire is 4×104joule/m3 then the Young's modulus of the material of the wire will be,
A1×1012N/m2B1.5×1012N/m2C2×1012N/m2D2.5×1012N/m2
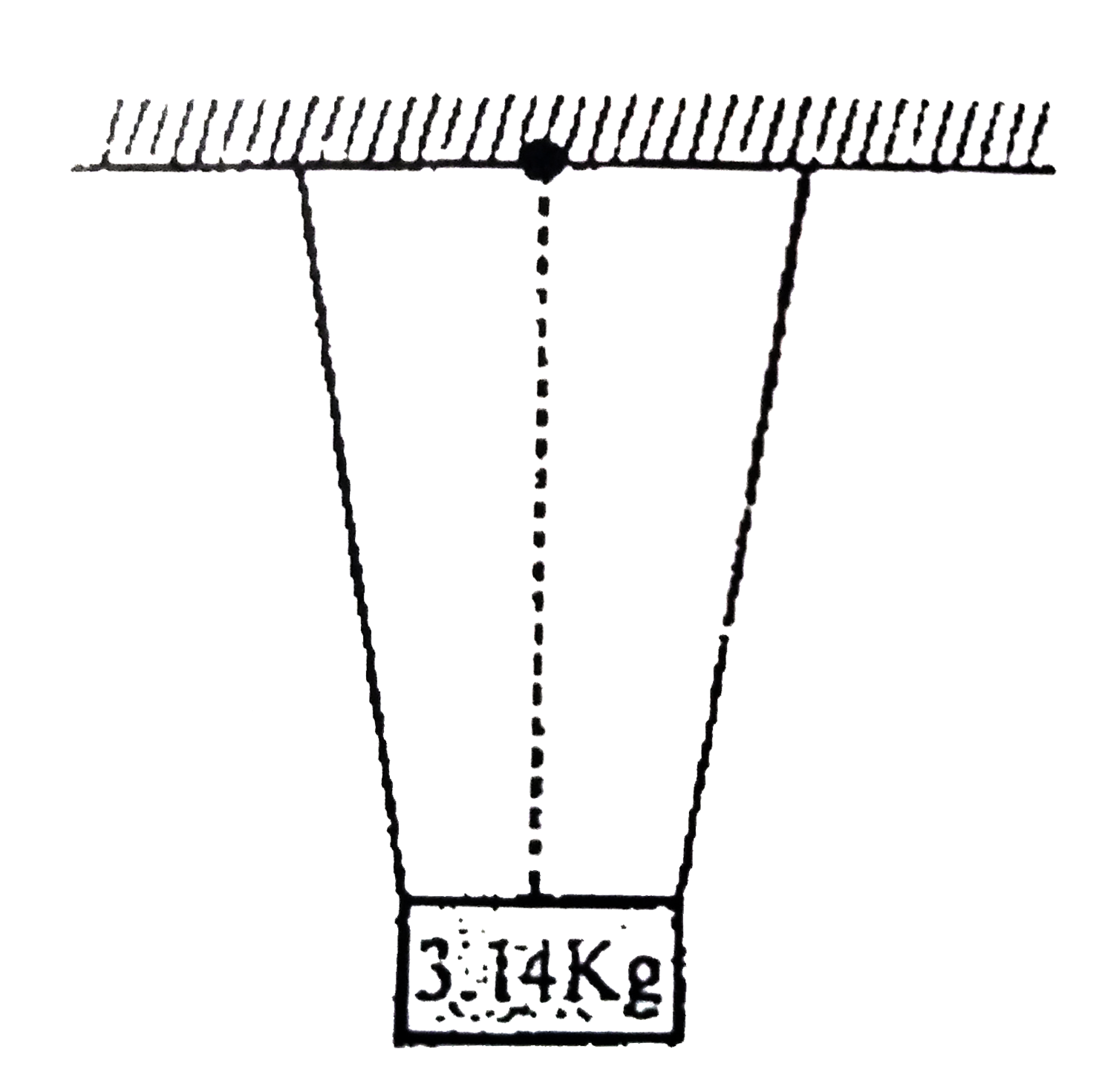
A body of mass 3.14 kg is suspended from one end of a non uniform wire of length 10m, such that the radius of the wire is changing uniformly from 9.8×10−4 m at one end to 5×10−4 m at the other end. Find the change in length of the wire in mm. Young's modulus of the material of the wire is 2×1011N/m2 (mass of wire is negligible)
 View Solution
View SolutionA uniform cylindrical wire is subjected to a longitudinal tensile stress of 5×107N/m2. Young's modulus of the material of the wire is 2×1011N/m2. The volume change in the wire is 0.02%. The factional change in the radius is
View SolutionOn applying a stress of 20×108N/m2 the length of a perfectly elastic wire is doubled. It Young's modulus will be
View SolutionA wire having a diameter of 3mm is stretched by an external force, to produce a longitudinal strain of 3×10−3. If the Poisson's ratio of the wire is 0.4, the change in the diameter is
View SolutionThe length of a wire is 1.0m and the area of cross-section is 1.0×10−2cm2. If the work done for increase in length by 0.2cm is 0.4 joule, then Young's modulus of the material of the wire is
View Solution

