A point tube is mounted on an aeroplane wing to measure the speed of the plane. The tube contains alcohol and shows a level difference of 40 cm. What is the speed of the plane reative to air ? (sp. Gr. Of alcohol = 0.8 and density of air = 1 kg m−3).
To find the speed of the plane relative to air using the information given, we can follow these steps:
Step 1: Understand the problem
We have a point tube mounted on an airplane wing that measures the speed of the plane. The tube contains alcohol, which shows a level difference of 40 cm. We need to find the speed of the plane relative to air.
Step 2: Convert the level difference to meters
The level difference given is 40 cm. We need to convert this to meters for our calculations:
Level difference=40cm=0.4m
Step 3: Calculate the density of alcohol
The specific gravity of alcohol is given as 0.8. The density of water is approximately 1000kg/m3. Therefore, the density of alcohol can be calculated as:
Density of alcohol=Specific gravity×Density of water=0.8×1000kg/m3=800kg/m3
Step 4: Apply Bernoulli's principle
According to Bernoulli's principle, the pressure difference can be expressed as:
P1−P2=12ρV2
where:
- P1−P2 is the pressure difference,
- ρ is the density of the fluid (in this case, air),
- V is the speed of the plane relative to air.
Step 5: Relate the pressure difference to the height of the alcohol column
The pressure difference can also be expressed in terms of the height of the alcohol column:
P1−P2=ρalcohol⋅g⋅h
where:
- ρalcohol=800kg/m3,
- g=9.8m/s2 (acceleration due to gravity),
- h=0.4m.
Calculating this gives:
P1−P2=800⋅9.8⋅0.4
P1−P2=3136Pa
Step 6: Set up the equation for speed
Now we can set the two expressions for pressure difference equal to each other:
3136=12⋅ρair⋅V2
Given that the density of air is 1kg/m3, we can substitute this into the equation:
3136=12⋅1⋅V2
Step 7: Solve for V
Rearranging the equation gives:
V2=2⋅3136
V2=6272
Taking the square root:
V=√6272≈79.18m/s
Final Answer
The speed of the plane relative to air is approximately 79.18m/s.
---
We have a point tube mounted on an airplane wing that measures the speed of the plane. The tube contains alcohol, which shows a level difference of 40 cm. We need to find the speed of the plane relative to air.
The level difference given is 40 cm. We need to convert this to meters for our calculations:
Level difference=40cm=0.4m
The specific gravity of alcohol is given as 0.8. The density of water is approximately 1000kg/m3. Therefore, the density of alcohol can be calculated as:
Density of alcohol=Specific gravity×Density of water=0.8×1000kg/m3=800kg/m3
According to Bernoulli's principle, the pressure difference can be expressed as:
P1−P2=12ρV2
where:
- P1−P2 is the pressure difference,
- ρ is the density of the fluid (in this case, air),
- V is the speed of the plane relative to air.
The pressure difference can also be expressed in terms of the height of the alcohol column:
P1−P2=ρalcohol⋅g⋅h
where:
- ρalcohol=800kg/m3,
- g=9.8m/s2 (acceleration due to gravity),
- h=0.4m.
P1−P2=800⋅9.8⋅0.4
P1−P2=3136Pa
Now we can set the two expressions for pressure difference equal to each other:
3136=12⋅ρair⋅V2
Given that the density of air is 1kg/m3, we can substitute this into the equation:
3136=12⋅1⋅V2
Rearranging the equation gives:
V2=2⋅3136
V2=6272
Taking the square root:
V=√6272≈79.18m/s
The speed of the plane relative to air is approximately 79.18m/s.
Topper's Solved these Questions
Similar Questions
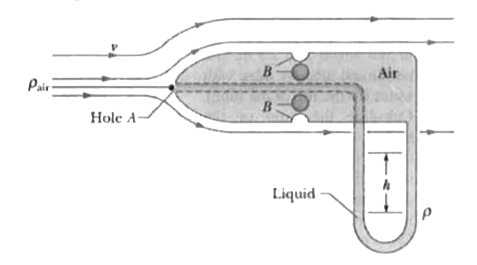
A pitot tube Fig. is used to determine the air speed of an airplane. It consists of an outer tube with a number of small holes B (four are shown that allow air into the tube, that tube is connected to one arm of a U-tube. The other arm of the U-tube is connected to hole A at the front end of the device, which points in the direction the plane is headed. At A the air becomes stagnant so that vA = 0. At B, however, the speed of the air presumably equals the airspeed v of the plane. (a) Use Bernoulli's equation to show that
v=√2ρghρair
where ρ is the density of the liquid in the U-tube and his the difference in the liquid levels in that tube. (b) Suppose that the tube contains alcohol and the level difference h is 20.0 cm. What is the plane's speed relative to the air? The density of the air is 1.03kg/m3 and that of alcohol is 810 kg/m3
 View Solution
View SolutionIn a test experiment on a model aeroplane in a wind tunnel, the flow speeds on the upper and lower surface of the wing are 70ms−1and63ms−1 respectivley. What is the lift on the wing if its area is 2.5m2? Take the density of air is 1.3kgm−3.
View Solution
Knowledge Check
- Question 1 - Select One
The speed of flow past the lower surface of a wing of an aeroplane is 50ms−1. What speed of flow over the upper surface will give a dynamic lift of 1000Pa? Density of air =1.3kgm−3
 A25.55m/sB63.55m/sC13.25m/sDNone of these
A25.55m/sB63.55m/sC13.25m/sDNone of these - Question 2 - Select One
In a test experiment on a model aeroplane in a wind tunnel, the flow speeds on the upper and lower surfaces of the wing are 70ms−1 and 83ms−1 respectively. What is the lift on the wing, if its area is 2.5m2? Take the density of air to be 1.3kgm−3
A1513NB1513 dinesC151.3 ND151.3 dynes - Question 3 - Select One
A plane is in level flight at constant speed and each of the two wings has an area of 25m2. If the speed of the air on the upper and lower surfaces of the wing are 270kmh−1 and 234kmh−1 respectively, then the mass of the plane is (take the density of the air = 1kgm−3)
A1550 kgB1750 kgC3500 kgD3200 kg
An aeronautical engineer observed that on the upper and the lower surface of the wing of an aeroplane the speed of the air are 120ms−1and90ms−1 respectively during flight. What is the lift on the wing of aeroplane if its area is 3.2m2? Given density of air is 1.29kg/m3.
View SolutionEach of the two wings of an aeroplane has area 30m2. The speed of the air on the upper and lower surfaces of theon the wing of aeroplane are 90ms−1 and 70ms−1 respectively. If the plane is in level flight at constant speed, find the uplift and the mass of the aeroplane. Given density of air =1.29kgm−3.
View SolutionA fully loaded Boeing aircraft has a mass of 3.3×105kg. Its total wing area is 500m2 . It is in level flight with a speed of 960km/h.
(a) Estimate the pressure difference between the lower and upper surfaces of the wings
(b) Estimate the fracitional increases in the speed of the air on the upper surfaces of the wing relative to the lower surface. The density of air is 1.2kg/m3.View SolutionA plane is in level flight at constant speed and each of its two wings has an area of 25m2 . If the speed of the air on the upper and lower surfaces of the wing are 270kmh−1 and 234kmh−1 respectively, then the mass of the plane is (Take the density of the air =1kgm−3)
View SolutionAir stream flows horizontally past an aeroplane wing of surface area 4m2. The speed of air over the top surface is 60ms−1 and under the bottom surface is 40ms−1 The force of lift on the wing is (density of air =1kgm−3)
View Solution

