The efficiency of otto cycle for petrol engine is 50% and the adiabatic constant is 1.4. calculate the compression ratio.
To solve the problem of calculating the compression ratio of an Otto cycle given the efficiency and the adiabatic constant, we can follow these steps:
1. Understand the Efficiency Formula:
The efficiency (η) of an Otto cycle is given by the formula:
η=1−1rγ−1
where:
- η = efficiency of the cycle
- r = compression ratio
- γ = adiabatic constant (given as 1.4)
2. Substitute the Known Values:
We know that the efficiency η=0.50 (50%) and γ=1.4. Substitute these values into the efficiency formula:
0.50=1−1r1.4−1
Simplifying the exponent:
0.50=1−1r0.4
3. Rearranging the Equation:
Rearranging the equation to isolate the term involving r:
1r0.4=1−0.50
1r0.4=0.50
4. Taking the Reciprocal:
Taking the reciprocal of both sides gives:
r0.4=2
5. Raising to the Power of 10.4:
To find r, raise both sides to the power of 10.4:
r=210.4
6. Calculating the Compression Ratio:
Calculate 210.4:
r=22.5=√25=√32≈5.656
Final Answer:
The compression ratio r is approximately 5.66.
---
The efficiency (η) of an Otto cycle is given by the formula:
η=1−1rγ−1
where:
- η = efficiency of the cycle
- r = compression ratio
- γ = adiabatic constant (given as 1.4)
We know that the efficiency η=0.50 (50%) and γ=1.4. Substitute these values into the efficiency formula:
0.50=1−1r1.4−1
Simplifying the exponent:
0.50=1−1r0.4
Rearranging the equation to isolate the term involving r:
1r0.4=1−0.50
1r0.4=0.50
Taking the reciprocal of both sides gives:
r0.4=2
To find r, raise both sides to the power of 10.4:
r=210.4
Calculate 210.4:
r=22.5=√25=√32≈5.656
The compression ratio r is approximately 5.66.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - SL ARORACHAPTER - THERMODYNAMICSEXERCISE - Problems from competitive examinations
22 Videos
- THERMODYNAMICSBOOK - SL ARORACHAPTER - THERMODYNAMICSEXERCISE - Problems for self practice
97 Videos
- Thermal Properties of MatterBOOK - SL ARORACHAPTER - Thermal Properties of MatterEXERCISE - Exercise
449 Videos
- Units and MeasurementsBOOK - SL ARORACHAPTER - Units and MeasurementsEXERCISE - Exercise
499 Videos
Similar Questions
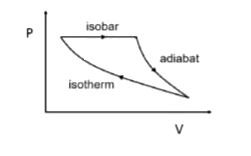
The efficiency of the cycle shown below in the figure ( consisting of one isobar , one adiabatic and one isotherm ( is 50 % the ratio ,x, between the highest and lowest temperature attained in this cycle obeys ( the working substance is an ideal gas )
View SolutionCalculate the efficiency of a cycle consisting of two isobaric and two adiabtic lines, if the pressure changes n=10 times within the cycle. The working substances is an ideal gas of adiabatic exponent γ=1.5.
View Solution
Knowledge Check
The efficiency of carnot engine is 50% and temperature of sink is 500K. If temperature of source is kept constant and its efficiency raised to 60%, then the required temperature of the sink will be : -
A100 KB600 KC400 KD500 KThe efficiency of Carnot engine is 50% and temperature of sink is 500 K. If temperature of source is kept constant and its efficiency raised to 60%, then the required temperature of sink will be
A100 KB600 KC400 KD500 KThe efficiency of carnot engine is 50% and temperature of sink is 500K. If temperature of source is kept constant and its efficiency raised to 60%, then the required temperature of the sink will be : -
A100 KB600 KC400 KD500 K
If the efficiency of an engine is 50% and its work output is 500 J then find input.
View SolutionThe efficiency of a heat engine is defined as the ratio of the mechanical work done by the engine in one cycle to the heat absorbed from the high temperature source . η=WQ1=Q1−Q2Q1 Cornot devised an ideal engine which is based on a reversible cycle of four operations in succession: isothermal expansion , adiabatic expansion. isothermal compression and adiabatic compression.
_E01_236_Q01.png)
For carnot cycle Q1T1=Q2T2. Thus η=Q1−Q2Q1=T1−T2T1 According to carnot theorem "No irreversible engine can have efficiency greater than carnot reversible engine working between same hot and cold reservoirs"._E01_236_Q02.png)
A carnot engine whose low temperature reservoir is at 7∘C has an efficiency of 50%. It is desired to increase the efficiency to 70%. By how many degrees should the temperature of the high temperature reservoir be increased?
View SolutionThe efficiency of a heat engine is defined as the ratio of the mechanical work done by the engine in one cycle to the heat absorbed from the high temperature source . η=WQ1=Q1−Q2Q1 Cornot devised an ideal engine which is based on a reversible cycle of four operations in succession: isothermal expansion , adiabatic expansion. isothermal compression and adiabatic compression.
_E01_237_Q01.png)
For carnot cycle Q1T1=Q2T2. Thus η=Q1−Q2Q1=T1−T2T1 According to carnot theorem "No irreversible engine can have efficiency greater than carnot reversible engine working between same hot and cold reservoirs"._E01_237_Q02.png)
An inventor claims to have developed an engine working between 600K and 300K capable of having an efficiency of 52%, then -
View SolutionThe efficiency of a heat engine is defined as the ratio of the mechanical work done by the engine in one cycle to the heat absorbed from the high temperature source . η=WQ1=Q1−Q2Q1 Cornot devised an ideal engine which is based on a reversible cycle of four operations in succession: isothermal expansion , adiabatic expansion. isothermal compression and adiabatic compression.
_E01_238_Q01.png)
For carnot cycle Q1T1=Q2T2. Thus η=Q1−Q2Q1=T1−T2T1 According to carnot theorem "No irreversible engine can have efficiency greater than carnot reversible engine working between same hot and cold reservoirs"._E01_238_Q02.png)
Efficiency of a carnot's cycle change from 16 to 13 when source temperature is raised by 100K. The temperature of the sink is-
View SolutionDetermine efficiency of carnot cycle if in adiabatic expansion volume 3 times of initial and r=1.5.
View Solution
