The total energy of rolling ring of mass m and radius R is
A
32mv2
B
12mv2
C
mv2
D
52mv2
Video Solution
Text Solution
The correct Answer is:C
E=Translational K.E.+Rotational K.E.
=1mv2+12Iω2=12mv2+12mR2.v2R2=mv2
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The total energy of rolling of mass 'm' and radius 'R' is
A3/2mv2B1/2mv2Cmv2D5/2mv2The escape velocity form the centre of a unifrom ring of mass M and radius R is :
A√2GMRB√GMRC√GM2RD√GMRFor a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMR
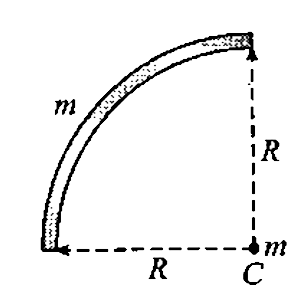
Find the force of attraction on a particle of mass m placed at the centre of a quarter ring of mass mand radius R as shown in figure.
View SolutionFind the kinetic energy needed to project a body of mass m from the centre of a ring of mass M and radius R so that it will never comne back.
View SolutionThe speed of rolling of a ring of mass m changes from V to 3V . What is the change in its kinetic energy
View SolutionMoment of inertia of a ring of mass M and radius R about a tangent to the circle of the ring is
View SolutionMoment of inertia of a ring of mass M and radius R about a tangent to the circle of the ring is
View Solution


