If P≡(a,a,) and Q=(−a,−a,−a), then the equation of the right bisecting plane of seg PQ is
x-y+z=a
x+y+z=3a
x+y+z=0
x+y+z+3a=0
The correct Answer is:C
Topper's Solved these Questions
- PLANE IN SPACE BOOK - MARVEL PUBLICATIONCHAPTER - PLANE IN SPACE EXERCISE - PREVIOUS YEAR MHT-CET EXAM QUESTIONS
3 Videos
- PLANE IN SPACE BOOK - MARVEL PUBLICATIONCHAPTER - PLANE IN SPACE EXERCISE - TEST YOUR GRASP- CHAPTERS 6,7,8
16 Videos
- PLANE IN SPACE BOOK - MARVEL PUBLICATIONCHAPTER - PLANE IN SPACE EXERCISE - TEST YOUR GRASP- CHAPTERS 6,7,22
1 Videos
- PAIR OF STRAIGHT LINESBOOK - MARVEL PUBLICATIONCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - TEST YOUR GRASP
19 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - MARVEL PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - MULTIPLE CHOICE QUESTIONS
39 Videos
Similar Questions
Knowledge Check
If P(¯p)=3i+j+2k and Q(¯q)=i−2j−4k the equation of plane passing through Q and perpendicular to line PQ is
A2x+3y + 6z+16=0Bx+y+z+7=0C2x+3y +6z+28=0D2x-3y+6z=15If Q is the image of the point P(2,3,4) under the reflection in the plane x−2y+5z=6 , then the equation of the line PQ is
Ax−2−1=y−32=z−45Bx−21=y−3−2=z−45Cx−2−1=y−3−2=z−45Dx−21=y−32=z−45The line PQ whose equation is x−y=2 cuts the x-axis at P,andQ is (4,2). The line PQ is rotated about P through 450 in the anticlockwise direction. The equation of the line PQ in the new position is y=−√2 (b) y=2 x=2 (d) x=−2
Ay=−√2By=2Cx=2Dx=−2
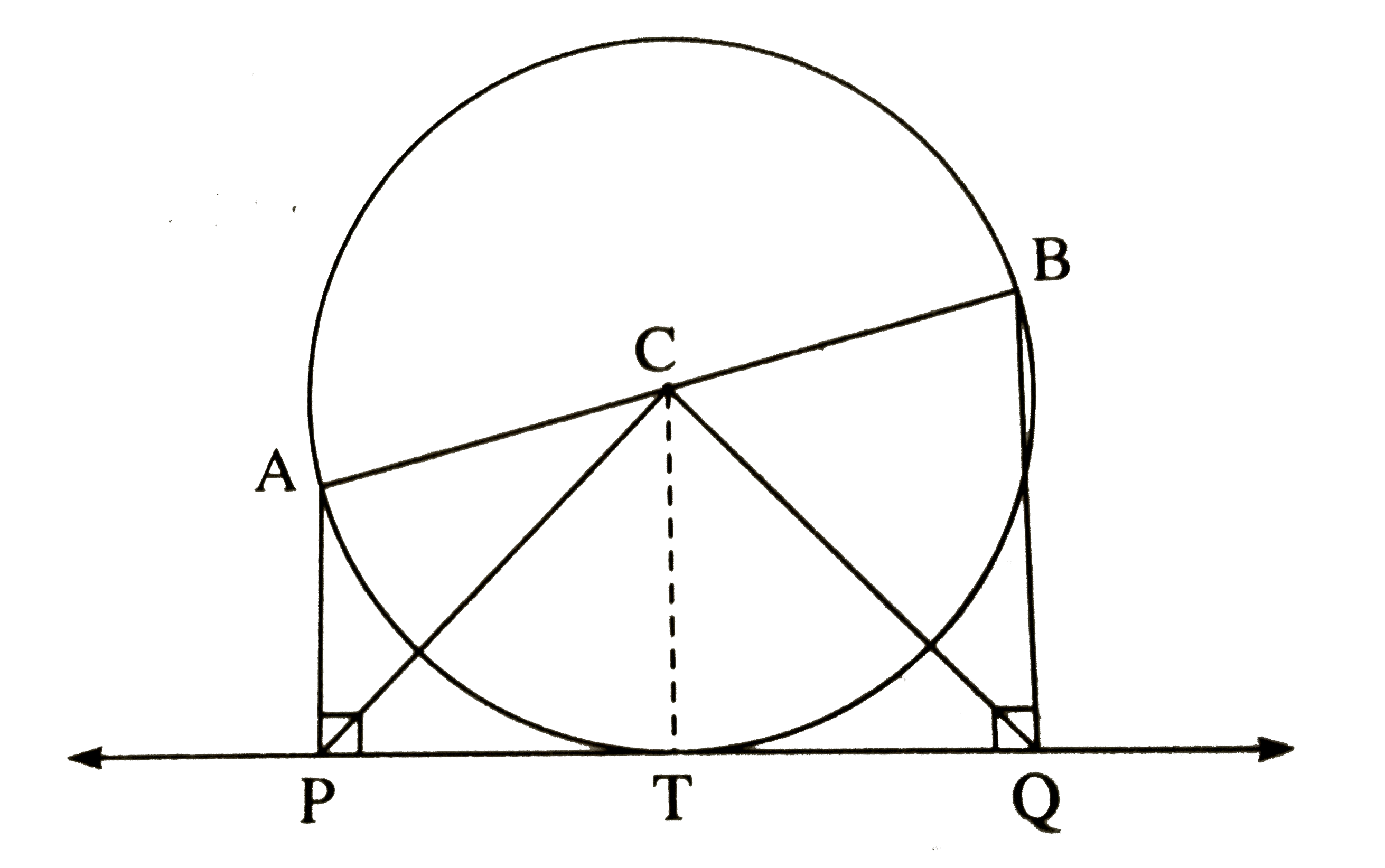
In the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent , which touches the circle at point T. seg AP⊥ line PQ and seg BQ⊥ line PQ.
Prove that, seg CP≅ seg CQ.

View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent, which touches the circle at point T. seg AP ⊥ line PQ and seg BQ ⊥ line PQ. Prove that, seg CP ≅ seg CQ.
View SolutionIf the roots of the equation lx2+mx+m=0 are in the ratio p:q, then
View SolutionEquation of the plane through the mid-point of the line segment joining the points P(4,6,−10)Q(−1,2,1) and perpendicular to PQ is
View SolutionEquation of the plane through the mid - point of the line segment joining the points P(4,5,-10) and Q (-1,2,1) and perpendicular to PQ is
View Solution
