Near room temperature , the thermo emf of a thermo couple is 40μV per degree. A galvanometer of 25Ω and capable of detecting current of the order of 4μ A is used. Calcualate the smallest temperature difference that can be detected with this galvanometer.
The correct Answer is:Use the relation , ɛ=αθ+12βθ∘
Step by step video, text & image solution for Near room temperature , the thermo emf of a thermo couple is 40 muV per degree. A galvanometer of 25 Omega and capable of detecting current of the order of 4 mu A is used. Calcualate the smallest temperature difference that can be detected with this galvanometer. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - THERMOELECTRICITYEXERCISE - Problem2videos
THERMOELECTRICITY
- BOOK - SL ARORACHAPTER - THERMOELECTRICITYEXERCISE - Problems for Self Practice13videos
THERMOELECTRICITY
- BOOK - SL ARORACHAPTER - SOLIDS AND SEMICONDUCTOR DEVICESEXERCISE - PROBLEM_TYPE9videos
SOLIDS AND SEMICONDUCTOR DEVICES
- BOOK - SL ARORACHAPTER - TRANSIENT CURRENTEXERCISE - Type D13videos
TRANSIENT CURRENT
Similar Questions
The thermo emf of a thermocouple is 40μVK−1 at room temperature. A galvanometer of resistance 100Ω capable of detecting current as law as 10μA is connected with one such thermocouple. Calculate the smallest temperature difference that can be detected by such a thermocouple.
View SolutionThe themo emf of a copper-constantan thermocouple is 40μV.∘C−1 at room temperature. A galvanometer whose resistance is 80Ω and current sensitivity 1μA is used. Find the smallest temperature difference that the galvanometer can detect.
View Solution
Knowledge Check
- Question 1 - Select One
The thermo e.m.f. of a thermo- couple is 25μV/∘C at room temperature. A galvanometer of 40 ohm resistance, capable of detecting current as low as 10−5A, is connected with the thermo couple. The smallest temperature difference that can be detected by this system is
A16∘CB12∘CC8∘CD20∘C - Question 2 - Select One
A thermocouple of negligible resistance produces an emf fo 40μV/∘C in the linear range of temperature. A galvanometer of resistance 10Ω whose sensitivity is 1μA/÷ is employed with the thermocouple. The smallest value of temperature difference that can be detected by the system will
A0.5∘CB1∘CC0.1∘CD0.25∘C - Question 3 - Select One
The smallest temperature difference that can be measured with a combination of a thermocouple of thermo e.m.f. 30μV per degree and a galvanometer of 50 ohm resistance, capable of measuring a minimum current of 3×10−7 amp is
A0.5 degreeB1.0 degreeC1.5 degreeD2.0 degree
Near room t emperature, the thermo emf of a copper constantan couple is 40μV per degree. What is the smallest temperature difference that can be detected with a single such couple and a galvanometer of 100 ohm resistance capable of detecting current as low 10−6 ampere?
View SolutionThe coil of a galvanometer is 0.02 × 0.08 m2. It consists of 200 turns of fine wire and is in a magnetic field of 0.2 tesla. The restoring torque constant of the suspension fibre is 10–6 Nm per degree. Assuming the magnetic field to be radial.
(i) What is the maximum current that can be measured by the galvanometer, if the scale can accommodate 30∘ deflection?
(ii) What is the smallest, current that can be detected if the minimum observable deflection is 0.1∘?View SolutionE.M.F. of a thermocouple is 25 mV/.∘C A galvanometer whose resistance is 40W, reads, 10−5A curren then minimum temperature which is determined by if will be
View SolutionII. Read the following text and answer the following questions on the basis of the same:
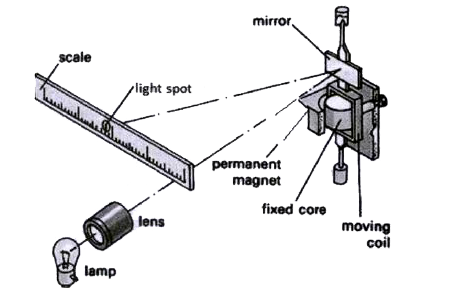
Galvanometer can sense/measure current. Improved mirror galvanometer was developed by William Thomson, later to become Lord Kelvin, in 1858. Thomson intended the instrument to read weak signal currents on very long submarine telegraph cables.
The fundamental problems of transmitting/receiving a singnal through a lengthy submarine cable was that the electrical current tended to be very low (as littles as 1/100,000th of a stadard light bulb). So, it was very difficult to detect it. To solve the problem it was thought that larger amount of electric current would be sent through the line. But Thomson had a different approach. He thought the best response was to devise a device that could read faint signals. The galvanometer, first invented in 1802, was a mean of detecting electric current. It consisted of a needle that was deflected by the magnetic field created by the electric current. But the galvanometers of the day could't detect the weak signals that came through a long underwater cable. But the improved version of galvanometer was highly sensitive to detect the lowest current. The mirror galvanometer consists of a long fine coil of silk-covered copper wire. In the heart of that coil, within a little air-chamber, a small round mirror is hung by a single fibre of floss silk, with four tiny magnets cemented to its back.
A beam of light is thrown from a lamp upon the mirror, and reflected by it upon a white screen or scale a few feet distant, where it forms a bright spot of light, when there is no current on the instrument, the spot of light remains stationary at the zero position on the screen, but the instant a current traverses the long wire of the coil, the suspended magnets twist themselves horizontally out of their former position, the mirror is inclined with them, and the beam of light is deflected along the screen to one side or the other, according to the nature of the current. If positive electric current gives a deflection to the right of zero, a negative current will give a deflection to the left of zero, and vice versa.
The air in the little chamber surrounding the mirror is compressed, so as to act like a cushion, and deaden the movements of the mirror, the mirror is thus prevented from idly swinging about at each deflections.
Mirror galvanometer galvabometer was primarily used to
 View Solution
View SolutionA thermocouple of resistance 1.6Ω is connected in series with a galvanometer of 8Ω resistance. The thermocouple develops and e.m.f. of 10μV per degree temperature difference between two junctions. When one junction is kept at 0∘C and the other in a molten metal, the galvanometer reads 8 millivolt . The temperature of molten metal, when e.m.f. varies linearly with temperature difference, will be
View Solution

