Show that the time for attaining half the value of the final steady current in LR-series circuit is 0.693(L/R).
Step by step video & image solution for Show that the time for attaining half the value of the final steady current in LR-series circuit is 0.693(L//R). by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - TRANSIENT CURRENTEXERCISE - Example37videos
TRANSIENT CURRENT
- BOOK - SL ARORACHAPTER - TRANSIENT CURRENTEXERCISE - Type A22videos
TRANSIENT CURRENT
- BOOK - SL ARORACHAPTER - TRANSIENT CURRENTEXERCISE - Type D13videos
TRANSIENT CURRENT
- BOOK - SL ARORACHAPTER - THERMOELECTRICITYEXERCISE - Problems for Self Practice13videos
THERMOELECTRICITY
- BOOK - SL ARORACHAPTER - UNIVERSEEXERCISE - PROBLEM_TYPE6videos
UNIVERSE
Similar Questions
Knowledge Check
- Question 1 - Select One
In L−C−R series circuit
Acurrent may achieve same value for two different value of frequencyBcurrent can not achieve same value for two different values of frequencyCcurrent is maximum for a maximum value of frequencyDnone of these - Question 2 - Select One
The current in the series L-C-R circuit is
Ai=imsin(ωt+ϕ)Bi=vm√R2+(Xc−XL)2sin(ωt+ϕ)Ci=2imcos(ωt+ϕ)DBoth (a) and (b) - Question 3 - Select One
At resonance the peak value of current in L−C−R series circuit is
AE0/RBE0√R2+(ωL−1ωC)2CE0√R2+(ωL−1ω2C∘)2DE0√2R
Does the steady state current in RL circuit depend upon L ?
View SolutionL.R. Circuit
View SolutionA coil of inductance 2H and resistance 10Ω are in a series circuit with an open key and a cell of constant 100V with negligible resistance. At time i=0, the key is closed. Find
(a) the time constant of the circuit.
(b) the maximum steady current in the circuit.
(c) the current in the circuit at f=1s.View SolutionShow that the sum of instantaneous currents during growth and decay of current in LR circuit is independent of time.
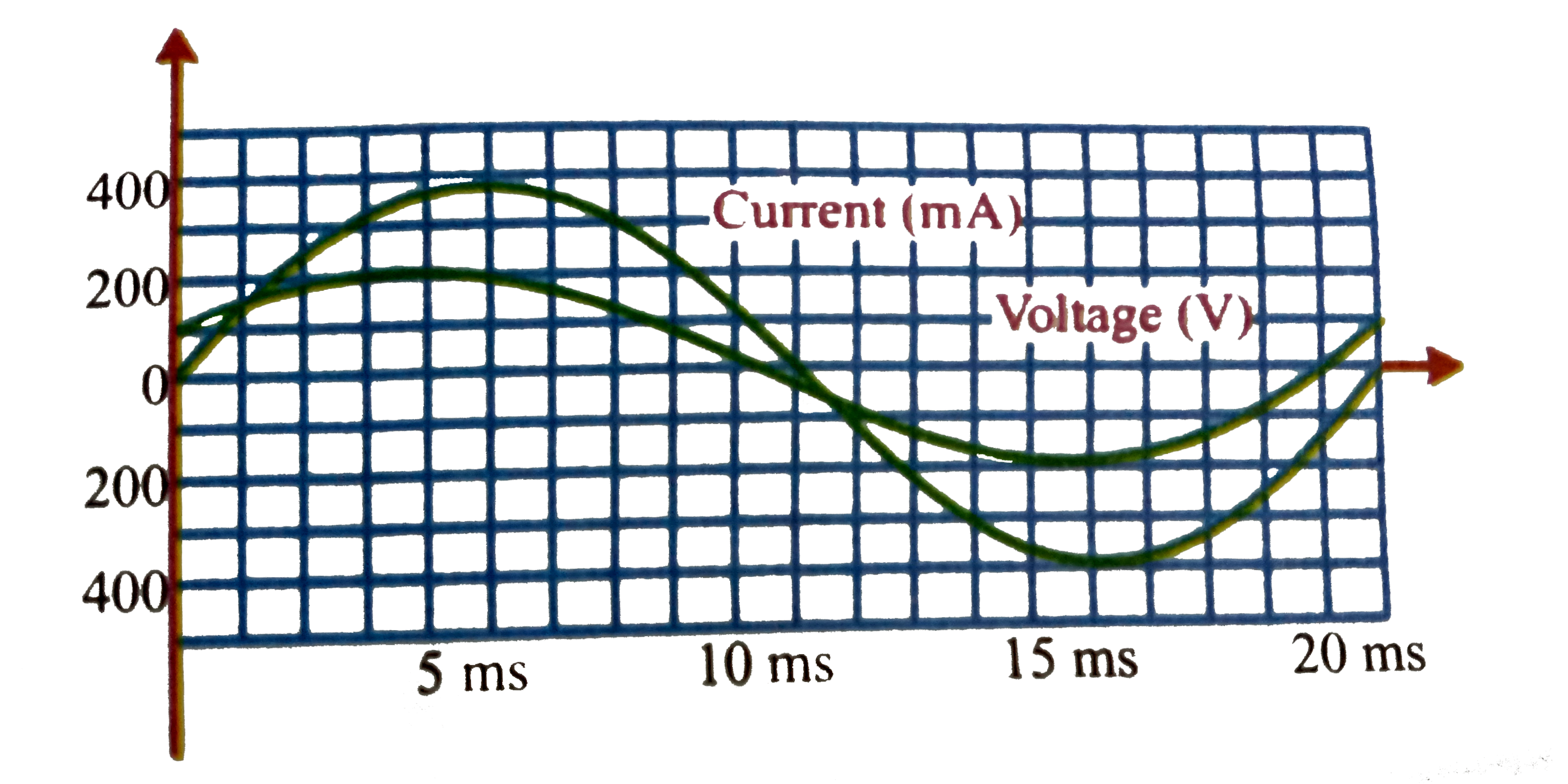
View SolutionThe given graph shows variation with time in the source voltage and steady state current drawn by a series RLC circuit. Given curve through origin is the current variation.
Which of the following statements is/are correct ?
 View Solution
View Solution


