An ancient building has a done of 5m radius and uniform but small thickness. The surface tension of its masionary structure is about 500Nm−1 . Treated as hemisphere, find the maximum load that dome can support.
The correct Answer is:(31420N)
To find the maximum load that the dome can support, we can use the relationship between surface tension, pressure, and force. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have a dome with a radius r=5m and a surface tension T=500N/m. We need to calculate the maximum load that this dome can support by treating it as a hemisphere.
Step 2: Calculate the Surface Area of the Hemisphere
The surface area A of a hemisphere is given by the formula:
A=2πr2
Substituting the radius:
A=2π(5)2=2π(25)=50πm2
Step 3: Calculate the Pressure Exerted by the Surface Tension
The pressure P exerted by the surface tension can be calculated using the formula:
P=4Tr
Substituting the values of T and r:
P=4×5005=20005=400N/m2
Step 4: Calculate the Maximum Force (Load) Supported by the Dome
The maximum force F that the dome can support is given by:
F=P×A
Substituting the values of P and A:
F=400×50π
Calculating this gives:
F=20000πN≈62831.85N
Conclusion
The maximum load that the dome can support is approximately 62831.85N.
---
We have a dome with a radius r=5m and a surface tension T=500N/m. We need to calculate the maximum load that this dome can support by treating it as a hemisphere.
The surface area A of a hemisphere is given by the formula:
A=2πr2
Substituting the radius:
A=2π(5)2=2π(25)=50πm2
The pressure P exerted by the surface tension can be calculated using the formula:
P=4Tr
Substituting the values of T and r:
P=4×5005=20005=400N/m2
The maximum force F that the dome can support is given by:
F=P×A
Substituting the values of P and A:
F=400×50π
Calculating this gives:
F=20000πN≈62831.85N
The maximum load that the dome can support is approximately 62831.85N.
Topper's Solved these Questions
Similar Questions
A steel cable with a radius of 1.5 cm support a chairlift at a ski area.if the maximum stress is not to exceed 108Nm−2, what is the maximum load the cable can support?
View SolutionThe lower end of a capillary tube of diameter 2.0 mm is dipped 8.00cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at temperature of the experiments is 7.30×10−2Nm−1. 1 atmospheric pressure =1.01×105Pa, density of water =1000kg/m3,g=9.80ms−2. also calculate the excess pressure.
View Solution
Knowledge Check
- Question 1 - Select One
The high domes of ancient buildings have structural value (besides beauty). It arises from pressure difference on the 2 faces due to curvature (as in soap bubbles). There is a dome of radius 5 m and uniform (but small ) thickness. The surface tension of its masonry structure is about 500 N/m. Treated as hemispherical, the maximum load that the dome can support is nearest to
A1500kg−WtB3000kg−WtC6000kg−WtD12000kg−Wt - Question 2 - Select One
Find out work done to expend soup bobble to radius R = 5 cm (surface tension of water = 0.1 N/m)
A2.8×10−3JB6.28×10−3JC3.7×10−3JD5.8×10−3J
Two capillaries of small cross section are connected as shown in the figure. The right tube has cross sectional radius R and left one has a radius of r(<R). The tube of radius R is very long where as the tube of radius r is of short length. Water is slowly poured in the right tube. Contact angle for the tube wall and water is θ=0∘. Let h be the height difference between water surface in the right and left tube. Surface tension of water is T and its density is ρ.
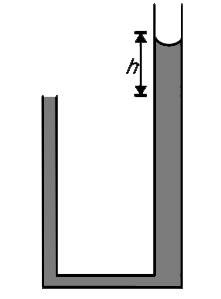
(a) Find the value of h if the water surface in the left tube is found to be flat.
(b) Find the maximum value of h for which water will not flow out of the left tube .View SolutionA satellite of mass m is going around the earth in a circular orbital at a height R2 from the surface of the earth. The satellite has lived its life and a rocket, on board, is fired to ake it leave the gravity of the earth. The rocket remains active for a very small interval of time and imparts an impulse in the direction of motion of the satellite. Neglect any hange in mass due to firing of the rocket. Find the minimum impulse imparted by the rocket to the satellite. Find the minimum work done by the rocket engine. Mass of the earth = M, Radius of the earth = R
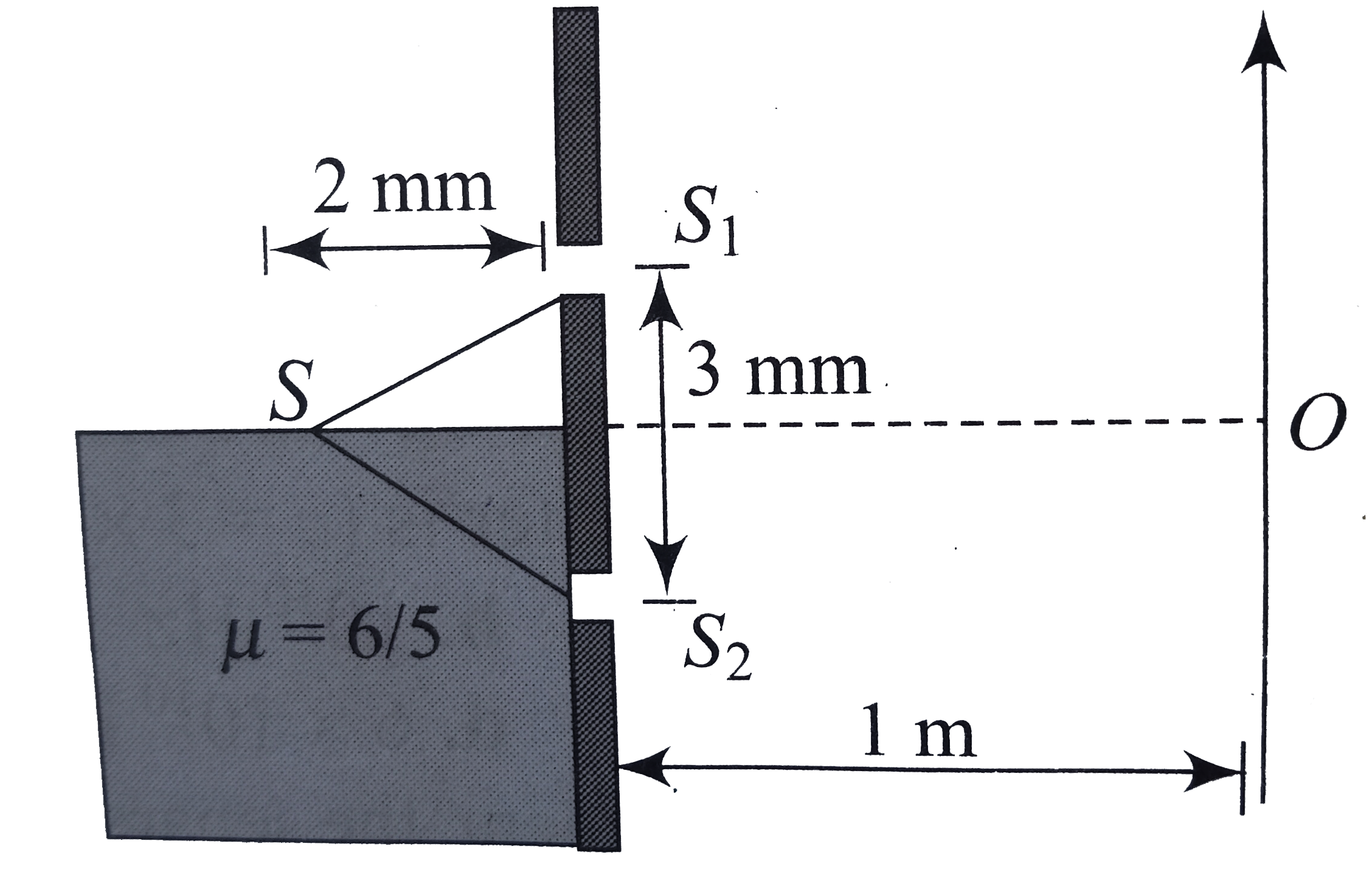
View SolutionIn Young's double-slit experiment, a point source is placed on a solid slab of refractive index 6/5 at a distance of 2 mm from two slits spaced 3 mm apart as shown and at equal distance from both the slits. The screen is at a distance of 1 m from the slits. Wavelength of light used is 500 nm.
a. Find the position of the central maximum.
b. Find the order of the fringe formed at O.
c. A film of refractive index 1.8 is to be placed in front of S1 so that central maxima is formed where 200th maxima was formed. Find the thickness of film.
 View Solution
View SolutionFind the work done in blowing a soap bubble of surface tension 0.06Nm−1 from 2 cm radius to 5 cm radius.
View SolutionA light rigid rod has a small ball of mass m attached to its one end. The other end is hinged on a table and the rod can rotate freely in vertical plane. The rod is released from vertical position and while falling the ball at its end strikes a hemisphere of mass m lying freely on the table. The collision between the ball and the hemisphere is elastic. The radius of hemisphere and length of the rod are R and 2R respectively. Find the velocity of the hemisphere after collision.
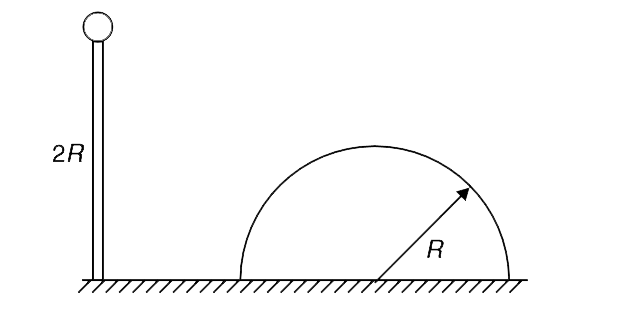 View Solution
View SolutionA structural steel rod has a radius of 10 mm and length of 1.0 m. A 100 kN force stretches it along its length. Young’s modulus of structural steel is 2×1011Nm_2. The percentage strain is about
View Solution

