A simple LR circuit is connected to a battery at time t=0. The energy stored in the inductor reaches half its maximum value at time
RLIn[√2√2−1]
RLIn[√2−1√2]
RLIn((√2√2−1)
RLIn[√2−1√2]
The correct Answer is:C
Step by step video, text & image solution for A simple LR circuit is connected to a battery at time t = 0. The energy stored in the inductor reaches half its maximum value at time by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Advance MCQs
33 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Conceptual MCQs
63 Videos
- CURRENT ELECTRICITYBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
389 Videos
- ELECTROSTATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Unsolved Numberical Problems
73 Videos
Similar Questions
The circuit is switched on at t=0, Find the time when energy stored in inductor becomes 1n tiimes of maximum energy stored in it:
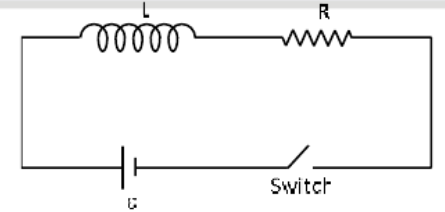
View SolutionA 35.0V battery with negligible internal resistance, a 50.0Ω resistor, and a 1.25mH inductor with negligible resistance are all connected in series with an open switch. The switch is suddenly closed
(a) How long after closing the switch will the current through the inductor reach one-half of its maximum value?
(b) How long after closing the switch will the energy stored in the inductor reach one-half of its maximum value?
View Solution
Knowledge Check
In an LR circuit connected to a battery, the rate at which energy is stored in the inductor is plotted against time during the growth of current in the circuit. Which of the following best represents the resulation curve?
A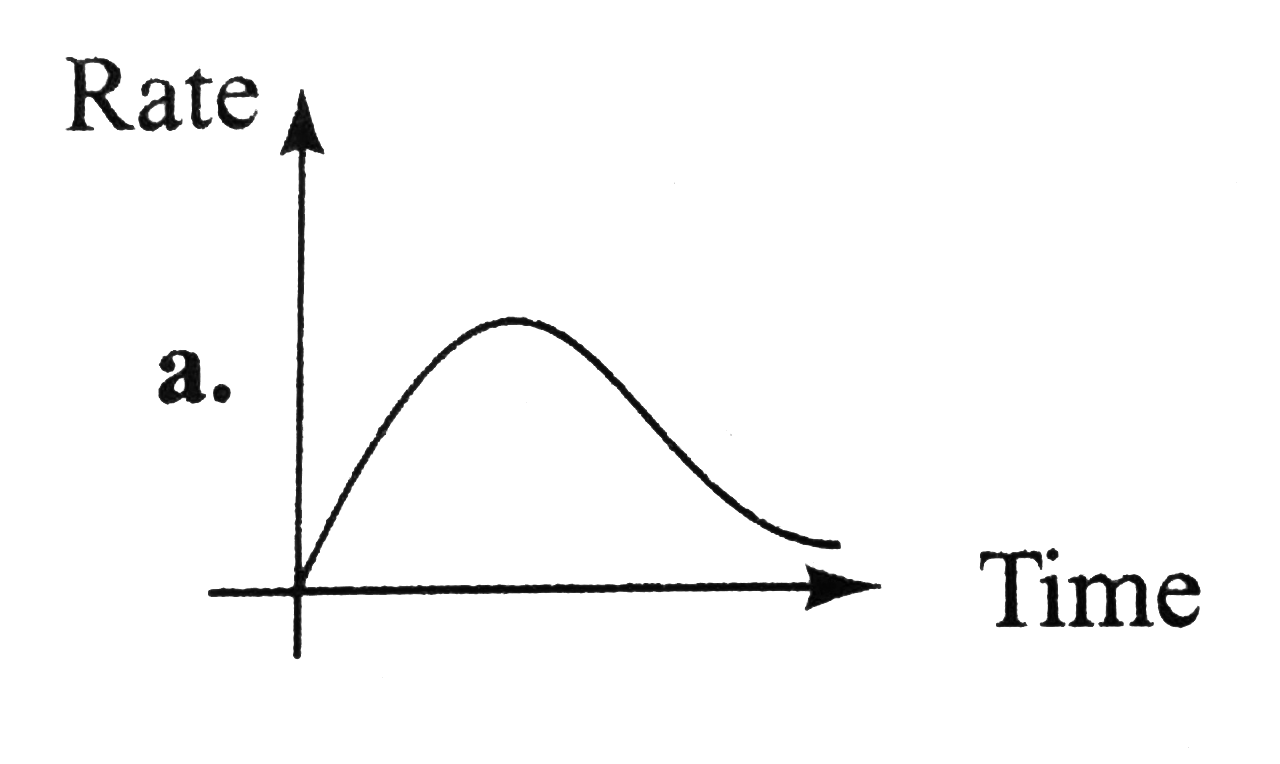 B
B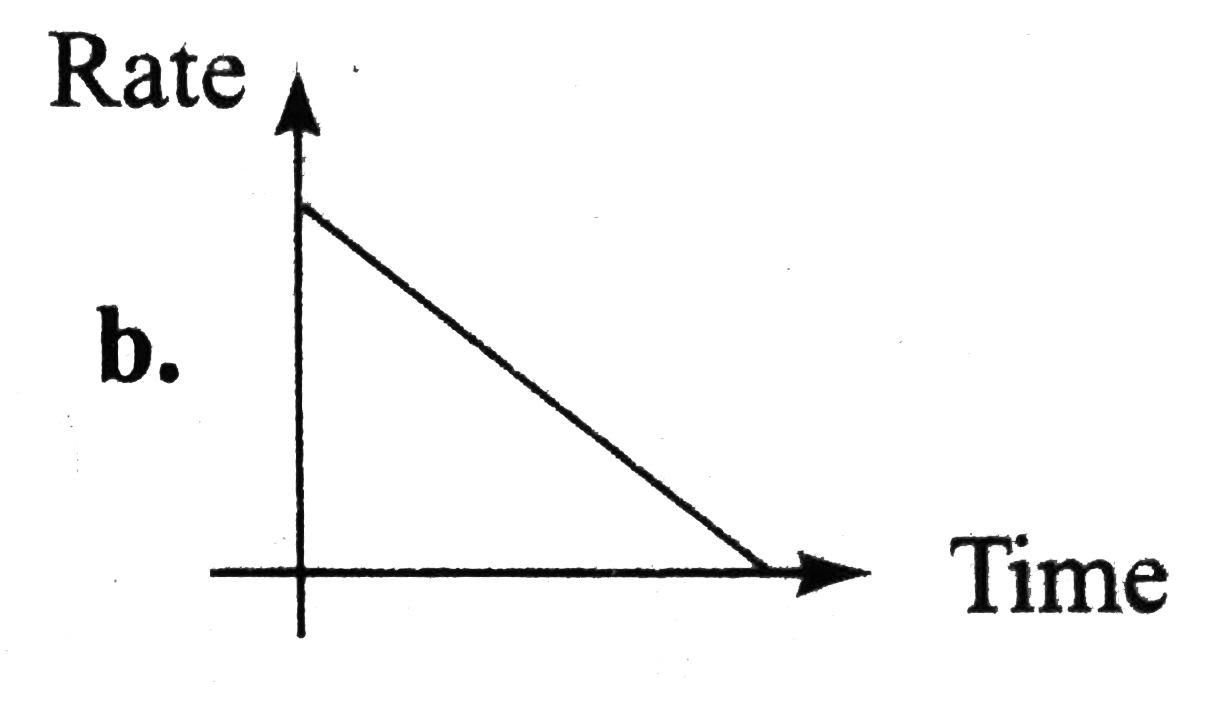 C
C D
D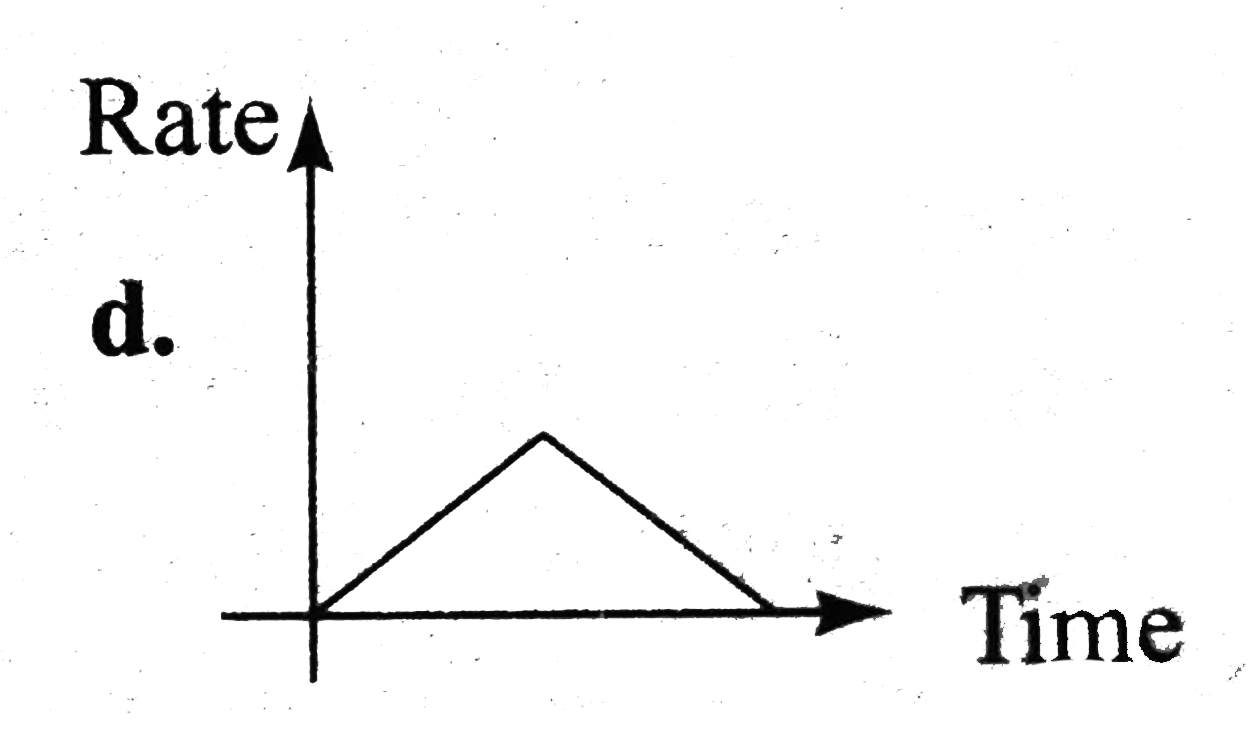
In a decaying L−R circuit, the time after which energy stores in the inductor reduces to one fourth of its initial values is
A(ln2)LRB0.5LRC√2LRD(√2√2−1)LRAn inductor in connected to an AC source . Magnetic field energy stored in inductor is found to change from its minimum value to maximum value in 10 ms. Frequency of AC source is
A25 Hz.B50 Hz.C75 Hz.D100 Hz.
A coil having an inductance L and a resistance R is connected to a battery of emfε. Find the time elapsed before (a) the current reaches half its maximum value, (b) the power dissipated in heat reaches half its maximum value and © the magnetic field energy stored in the circuit reaches half its maximum value.
View SolutionIn a chrging cirucit, after how many time constant will the energy stored in the capacitor reach one - half of its equilibrium value?
View SolutionAn L−C circuit consists of an inductor with L=0.0900H and a capacitor of C=4×10−4F. The initial charge on the capacitor is 5.00μC, and the initial current in the inductor is zero.
(a) What is the maximum voltage across the capacitor?
(b) What is the maximum current in the inductor?
(c) What is the maximum energy stored in the inductor?
(d) When the current in the inductor has half its maximum value, what is the charge on the capacitor and what is the energy stored in the inductor?
View SolutionA coil having an inductance L and a resistance R is connected to a battery of emf E . Find the time taken for the magnetic energy stored in the circuit to change from one fourth of the steady-state value.
View SolutionHow many time constants will elapse before the energy stored in the capacitor reaches half of its equilibrium value in a charging RC circuit ?
View Solution
