The angle between electric field intensity →E and the area vector →ds at which the T.N.E.I. is maximum is
π6
π2
zero
π3
The correct Answer is:C
Step by step video, text & image solution for The angle between electric field intensity vec(E) and the area vector vec(ds) at which the T.N.E.I. is maximum is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - CRITICAL THINKING67videos
ELECTROSTATICS
- BOOK - TARGET PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - COMPETITIVE THINKING124videos
ELECTROSTATICS
- BOOK - TARGET PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EVALUATION TEST8videos
ELECTROMAGNETIC INDUCTION
- BOOK - TARGET PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EVALUATION TEST24videos
GRAVITATION
Similar Questions
The sine of the angle between the vectors →i+3→j+2→k and 2→i−4→j+→k is
View SolutionAn electric dipole is placed in an electric field. Column I is the description of electric field and the angle between the dipole moment →p and the electric field intensity →E and Column II gives the effect of the field on the dipole. Then,
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Electric flux in an electric field →E through area vector →ds is given by
A→E×→dsB→E⋅→dsC→E/→dsD→ds/→E - Question 2 - Select One
The angle between vectors (→M×→N) and (→N×→M) is
A0∘B60∘C90∘D180∘ - Question 3 - Select One
An electric dipole is placed in a uniform electric field →E of magnitude 40N/C. Graph shows the magnitude of the square on the dipole versus the angle θ between the field →E and the dipole moment →p. The magnitude of dipole moment →p is equal to:
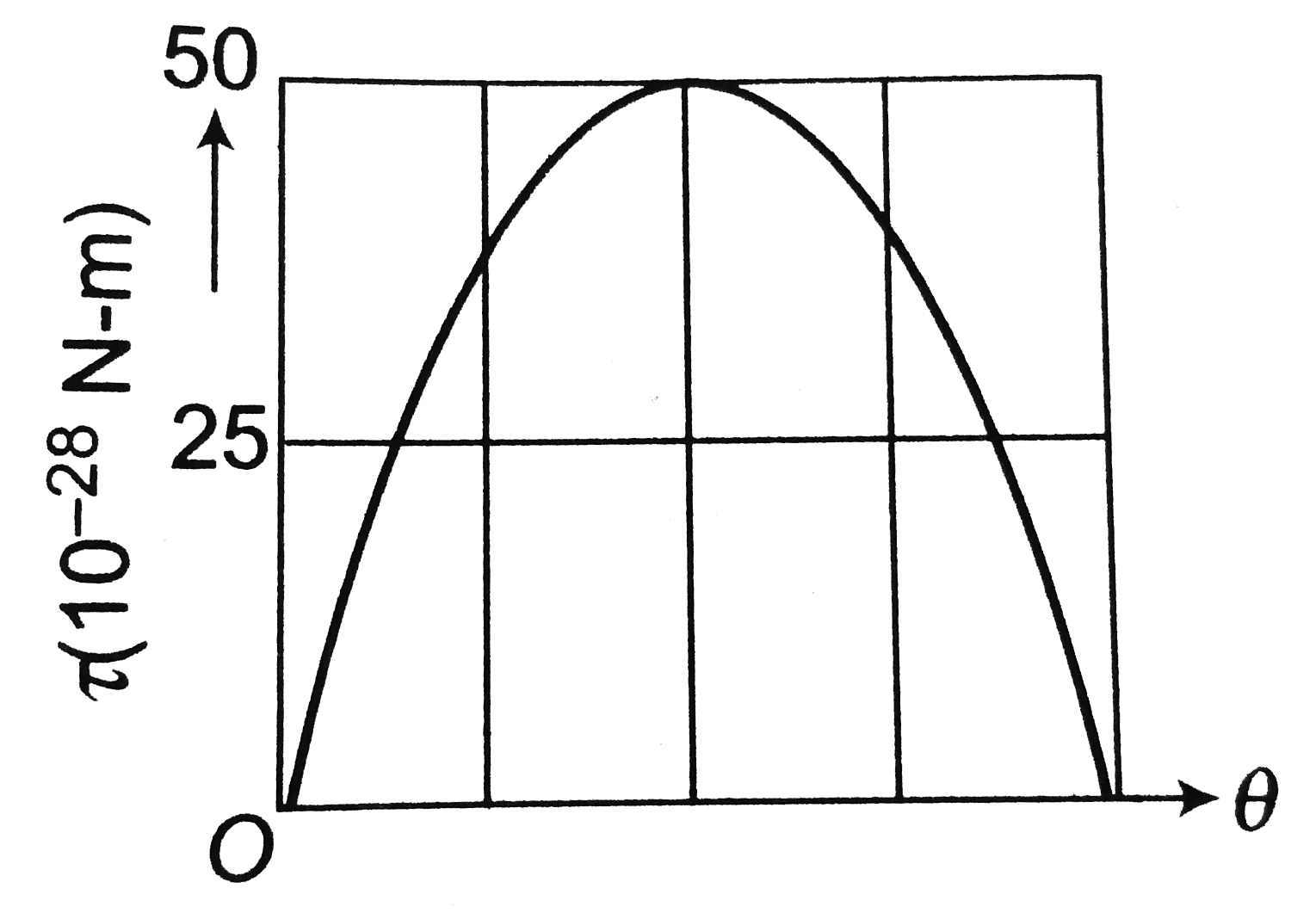 A1.25×10−28C−mB2.0×10−25C−mC2.5×10−28C−mD5.0×10−28C−m
A1.25×10−28C−mB2.0×10−25C−mC2.5×10−28C−mD5.0×10−28C−m
Find the angle between two vectors →a and →b, if ∣∣→a×→b∣∣=→a.→b .
View SolutionStatement - I : If a charge enters in electric field then it moves in the direction of →E
Statement - II : Force on charge is in the direction of field.View SolutionThe electric field intensity →E , , due to an electric dipole of dipole moment →p , at a point on the equatorial line is :
View SolutionWhen dipole moment →p of a dipole is parallel to electric field intensity →E (stable equilibrium) the potential energy of dipole is
View SolutionWhen dipole moment →P of a dipole is anti parallel to electric field intensity →E (unstable equilibrium), the potential energy of dipole is
View Solution

