Two identical capacitors, have the same capacitance C. One of them is charged to potential V1 and the other V2. The negative ends of the capacitors are connected together. When the poistive ends are also connected, the decrease in energy of the combined system is
14C(V21−V22)
14C(V21+V22)
14C(V1−V2)2
14C(V2−V1)2
The correct Answer is:C
Step by step video, text & image solution for Two identical capacitors, have the same capacitance C. One of them is charged to potential V_1 and the other V_2. The negative ends of the capacitors are connected together. When the poistive ends are also connected, the decrease in energy of the combined system is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - COMPETITIVE THINKING124videos
ELECTROSTATICS
- BOOK - TARGET PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - EVALUATION TEST14videos
ELECTROSTATICS
- BOOK - TARGET PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - EVALUATION TEST14videos
ELECTROSTATICS
- BOOK - TARGET PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EVALUATION TEST8videos
ELECTROMAGNETIC INDUCTION
- BOOK - TARGET PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EVALUATION TEST24videos
GRAVITATION
Similar Questions
Two capacitors of capacitances 3μF&6μF are charged to potential of 2V and 5V respectively.These two charged capacitors are connected in series.Find the potential across C1
View SolutionTwo capacitors of capacitances 3μFand6μF, are charged to potentials 2V and 5V respectively. These two charged capacitors are connected in series. Find the potential across each of the two capacitors now.
View Solution
Knowledge Check
- Question 1 - Select One
Two identical capacitors are joined in parallel, charged to a potential V and then separated and then connected in series i.e. the positive plate of one is connected to negative of the other
AThe charges on the free plates connected together are destroyedBThe charges on the free plates are enhancedCThe energy stored in the system increasesDThe potential difference in the free plates becomes 2V - Question 2 - Select One
A parallel plate capacitor of capacitance C is connected to a battery and is charged to a potential difference V. Another capacitor of capacitance 2C is ismilarly charged to a potential difference 2V. The charging battery is now disconnected and the capacitors are connected in parallel to each other in such a way that the poistive terminal of one is connected to the negative terminal of the other. The final energy of the configuration is
A(a) zeroB(b) 32CV2C(c) 256CV2D(d) 92CV2 - Question 3 - Select One
Two identical capacitors eachof capacitance C are charged to the same potential V and are connected in two circuits (i) and (ii) at t=0 as shown. The charges on the capacitor at t=CR are
 ACVe,CVeBCV, CVCVCe,VCDVC,VCe
ACVe,CVeBCV, CVCVCe,VCDVC,VCe
A capacitor of capacitance 6μF is charged to a potential of 150V. Its potential falls to 90V, when another uncharged capacitor is connected to it. Find the capacitance of the second capacitor and the amount of energy lost due to the connection.
View SolutionTwo capacitor of capacitance 2μFand3μF respectively are charged to potential difference 20 V each. Now the capacitors are connected such that the positively chargd plate of one capacitory is connected to the negatively charged plate of the other. after the current in the circuit has become negligible, the potential difference across the 2μF capacitor is ____V.
View SolutionTwo identical capacitors each of capacitance C are charged to the same potential V and are connected in two circuits (i) and (ii) at t=0 as shown. The charged on the capacitor at t=CR are
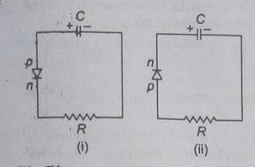 View Solution
View SolutionTwo identical capacitors each of capacitance C are charged to the same potential V and are connected in two circuits (i) and (ii) at t=0 as shown. The charged on the capacitor at t=CR are
 View Solution
View SolutionTwo capacitors of capacitances 1μFand3μF are charged to the same voltages 5V. They are connected in parallel with oppositely charged plates connected together. Then
View Solution

