A cylindrical capacitor has charge Q and length L. If both the charge and length of the capacitor are doubled by keeping other parameters fixed, the energy stored in the capacitor
remains same.
increases two times.
dereases two times.
increases four times.
The correct Answer is:B
To solve the problem step by step, we need to analyze how the energy stored in a cylindrical capacitor changes when both the charge and the length are doubled.
Step 1: Understand the formula for energy stored in a capacitor
The energy (U) stored in a capacitor is given by the formula:
U=12Q2C
where Q is the charge and C is the capacitance.
Step 2: Determine the capacitance of a cylindrical capacitor
The capacitance C of a cylindrical capacitor can be expressed as:
C=2πϵ0Lln(BA)
where:
- ϵ0 is the permittivity of free space,
- L is the length of the capacitor,
- A and B are the inner and outer radii of the cylindrical capacitor.
Step 3: Substitute the capacitance into the energy formula
Substituting the expression for capacitance into the energy formula, we get:
U=12Q22πϵ0Lln(BA)
This simplifies to:
U=Q2ln(BA)4πϵ0L
Step 4: Analyze the changes when charge and length are doubled
Now, if we double the charge and length:
- New charge Q′=2Q
- New length L′=2L
Step 5: Substitute the new values into the energy formula
The new energy U′ can be calculated as follows:
U′=(2Q)2ln(BA)4πϵ0(2L)
This simplifies to:
U′=4Q2ln(BA)8πϵ0L
U′=Q2ln(BA)2πϵ0L
Step 6: Relate the new energy to the original energy
Now, we can relate U′ to the original energy U:
U′=2⋅Q2ln(BA)4πϵ0L
U′=2U
Conclusion
Thus, the energy stored in the capacitor doubles when both the charge and length of the capacitor are doubled.
Final Answer
The energy stored in the capacitor becomes 2U.
The energy (U) stored in a capacitor is given by the formula:
U=12Q2C
where Q is the charge and C is the capacitance.
The capacitance C of a cylindrical capacitor can be expressed as:
C=2πϵ0Lln(BA)
where:
- ϵ0 is the permittivity of free space,
- L is the length of the capacitor,
- A and B are the inner and outer radii of the cylindrical capacitor.
Substituting the expression for capacitance into the energy formula, we get:
U=12Q22πϵ0Lln(BA)
This simplifies to:
U=Q2ln(BA)4πϵ0L
Now, if we double the charge and length:
- New charge Q′=2Q
- New length L′=2L
The new energy U′ can be calculated as follows:
U′=(2Q)2ln(BA)4πϵ0(2L)
This simplifies to:
U′=4Q2ln(BA)8πϵ0L
U′=Q2ln(BA)2πϵ0L
Now, we can relate U′ to the original energy U:
U′=2⋅Q2ln(BA)4πϵ0L
U′=2U
Thus, the energy stored in the capacitor doubles when both the charge and length of the capacitor are doubled.
The energy stored in the capacitor becomes 2U.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - TARGET PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - EVALUATION TEST
14 Videos
- ELECTROSTATICSBOOK - TARGET PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - CRITICAL THINKING
67 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - TARGET PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EVALUATION TEST
8 Videos
- GRAVITATIONBOOK - TARGET PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EVALUATION TEST
24 Videos
Similar Questions
Knowledge Check
A cylindrical capacitor has charge Q and length L. If both the charge and length of the capacitor are doubled by keeping other parameters fixed, the energy stored in the capacitor
Aemains sameBincreasestwo timesCdecreases two timesDincreases four timesIn a charged capacitor, the energy is stored in
Athe negative chargesBthe positive chargesCthe field between the platesDboth 'a' and 'b'In a charged capacitor the energy is stored in
Apositive chargeBboth in positive and negative chargeCthe electric field between the platesDthe edges of the capacitor plates
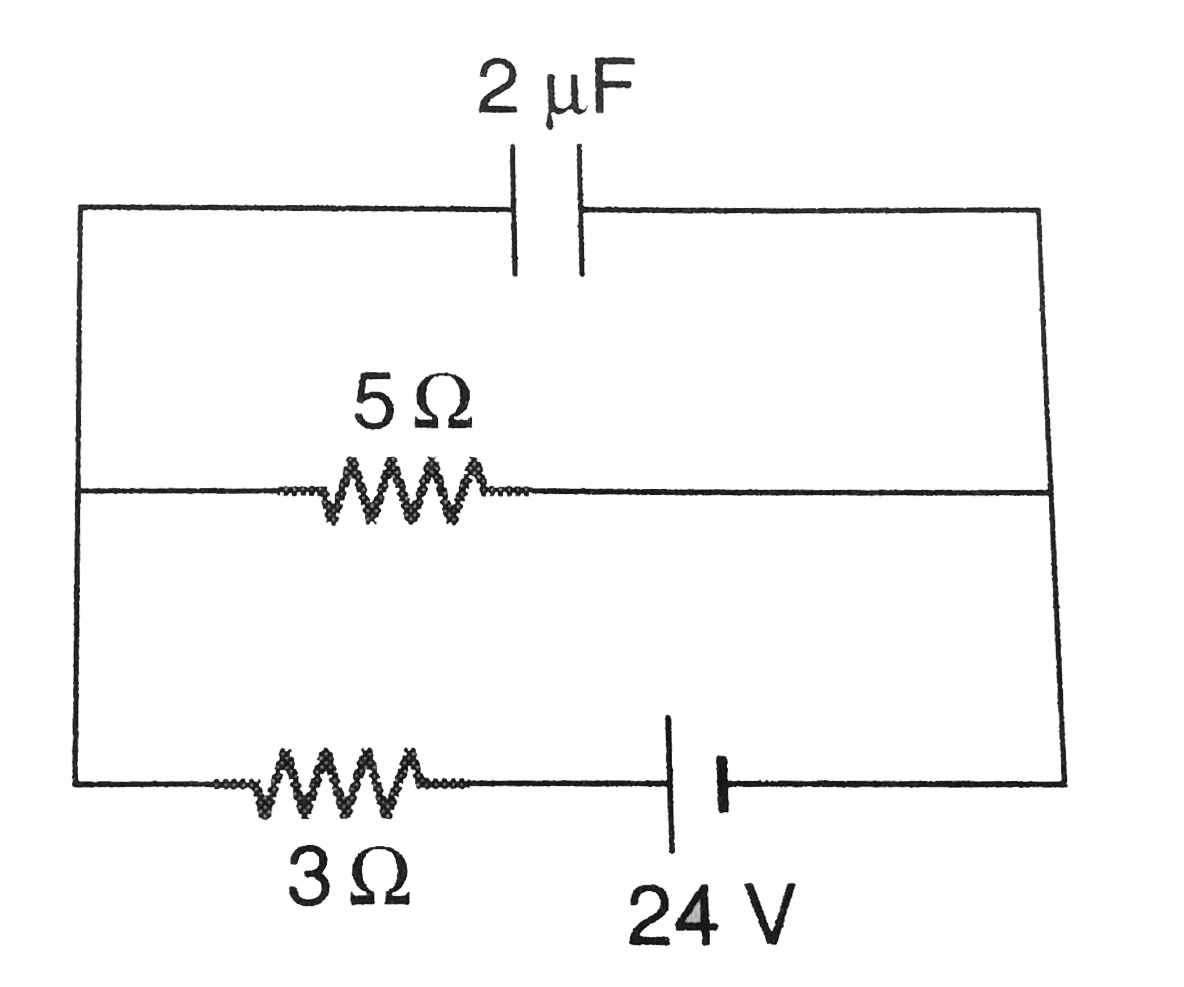
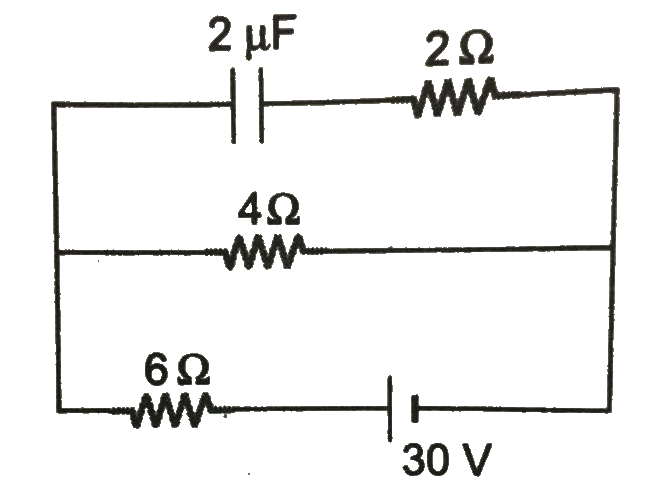
Find the charge stored in the capacitor.
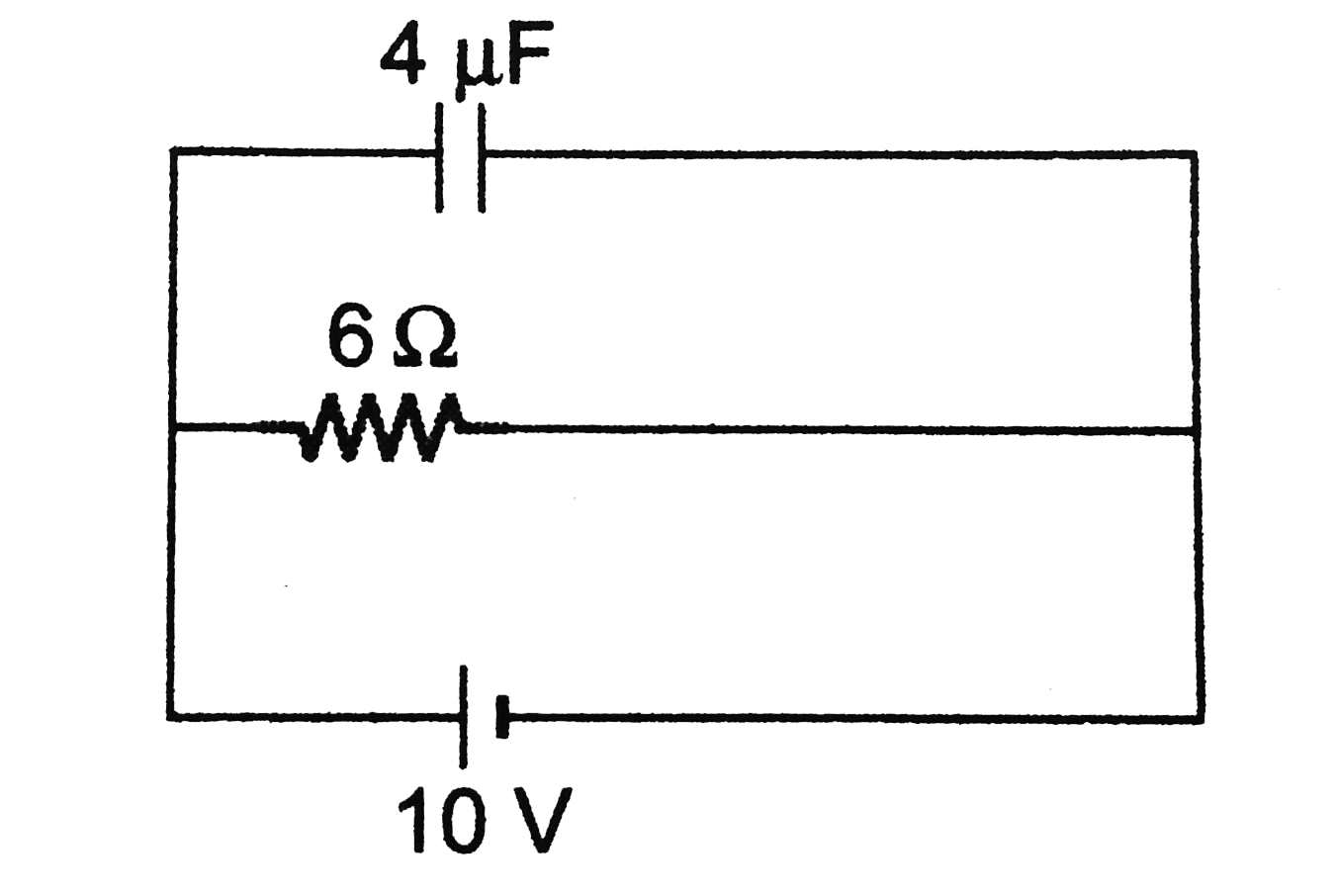
View SolutionFind the charged stored in all the capacitors
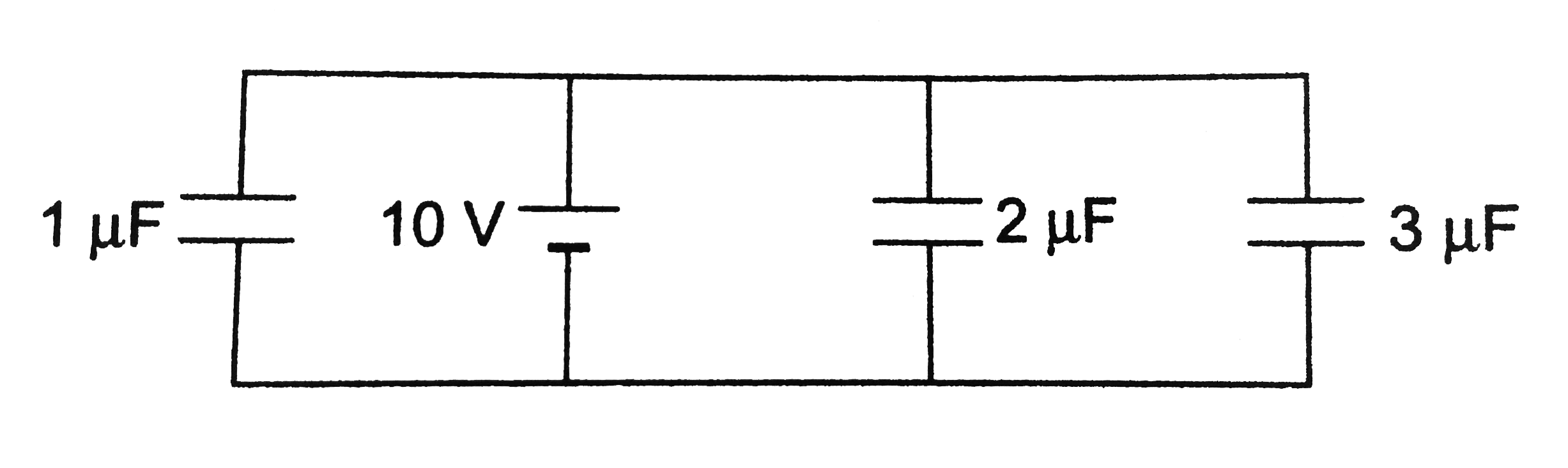
View SolutionFind the steady state charge stored in the capacitor.

View SolutionFind the steady state charge stored in the capacitor.
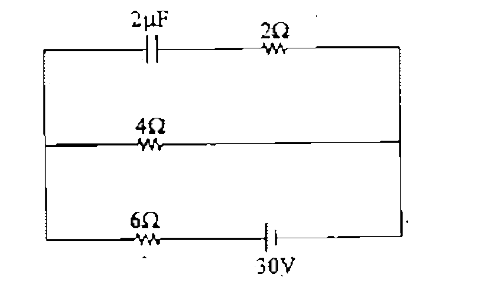
View SolutionThe total electrostatic energy stored in both the capacitor is
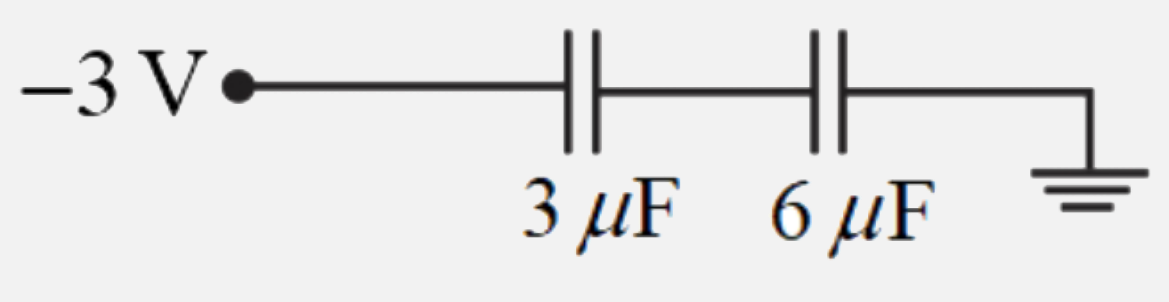
View Solution