
A woman 5 feet tall stands near a street near a street lamp that is 12 feet tall, as shown in the figure above . Find a formula that expresses l, the length of her shadow , in terms of d , her distance from the base of the lamp.
l=512d
l=513d
l=57d
l=1213d
The correct Answer is:C
Step by step video, text & image solution for A woman 5 feet tall stands near a street near a street lamp that is 12 feet tall, as shown in the figure above . Find a formula that expresses l, the length of her shadow , in terms of d , her distance from the base of the lamp. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A man of height 'h' is walking away from a street lamp with a constant speed 'v'. The height of the street lamp is 3h. The rate at which the length of the man's shadow is increasing when he is at a distance 10 h from the base of the street lamp is
View SolutionA man 2m tall, walks at the rate of 123m/sec towards a street light which is 513 m above the ground. At what rate is tip of his shadow moving? At what rate is the length of the shadow changing when he is 3113m from the base of the light?
View Solution
Knowledge Check

A lighthouse is built on the edge of a cliff near the ocean, as shown in the diagram above. From a boat located 200 feet from the base of the cliff, the angle of elevation to the top of the cliff is 18∘ and the angle of elevation to the top of the lighthouse is 28∘. Which of the following equations could be used to find the height of the lighthouse, x, in feet?Ax=200tan10∘Bx=200(tan28∘−tan18∘)Cx=200tan28∘−tan18∘Dx=200(tan18∘tan28∘)
When designing a stairway, an architect can use the riser-tread formula 2h + d = 25, where h is the riser height, in inches, and d is the tread depth, in inches. For any given stairway, the riser heights are the same and the tread depths are the same for all steps in that stairway. The number of steps in a stairway is the number of its risers. For example, there are 5 steps in the stairway in the figure above. The total rise of a stairway is the sum of the riser heights as shown in the figure.
An architect wants to use the riser-tread formula to design a stairway with a total rise of 9 feet, a riser height between 7 and 8 inches, and an odd number of steps. With the architect’s constraints, which of the following must be the tread depth, in inches, of the stairway? (1 foot = 12 inches)A7.2B9.5C10.6D15
A man 2m tall, walks at the rate of 123m/sec towards a street light which is 513 m above the ground. At what rate is tip of his shadow moving? At what rate is the length of the shadow changing when he is 3113m from the base of the light?
View SolutionA lamp is 3.3 m be the lamp post and CD= 110 cm tall walks away from the base of this lamp post at a speed of 0.8 m/s. find the length of the shadow of boy after 4 seconds.
View SolutionA fluorescent lamp of length 1m is placed horizontally at a depth of 1.2m below a ceiling . A plane mirror of length 0.6m is placed below the lamp parallel to and symmetric to the lamp at a distance 2.4m from it as shown in figure. Find the length in meters (distance between the extreme points of the visible region along x-axis ) of the reflected patch of light on the ceiling.
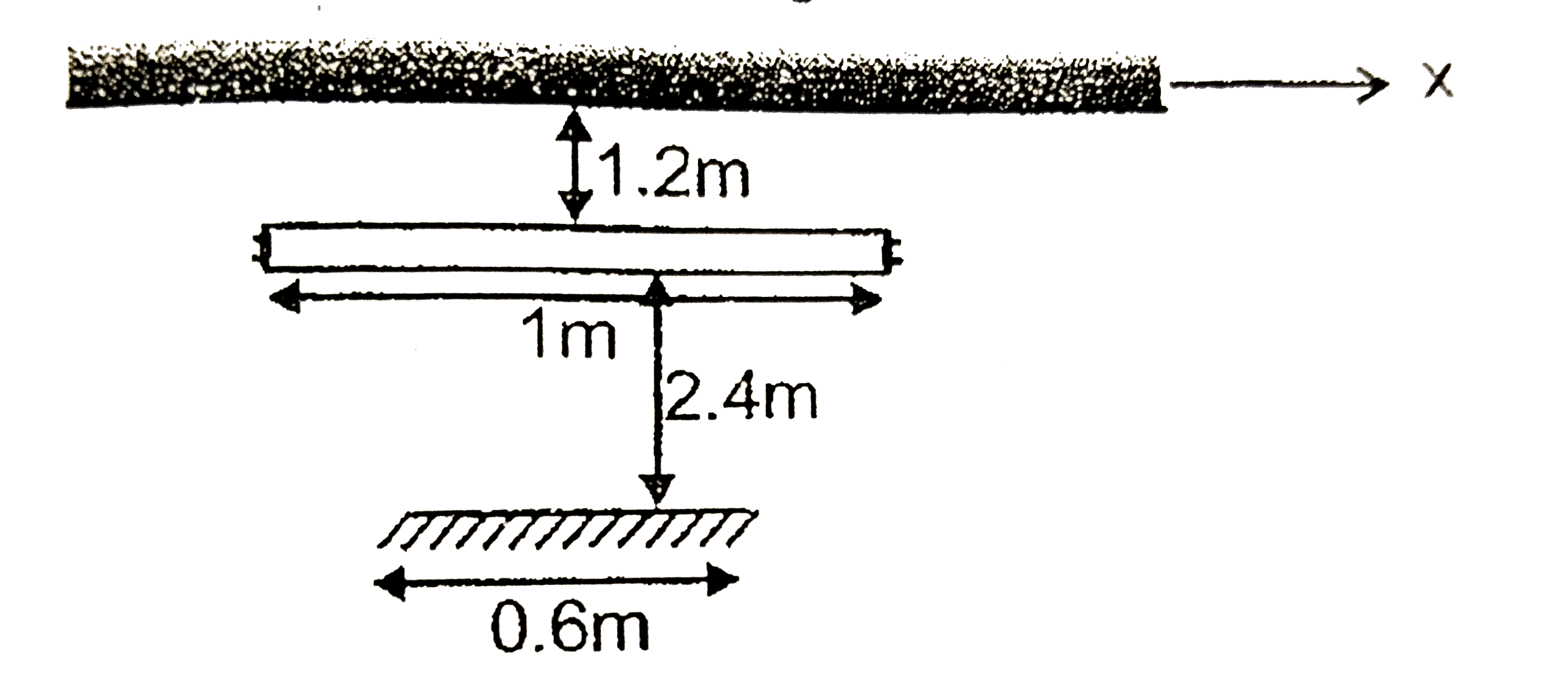
View SolutionA lamp post of length 10 meter placed at the end A of a ladder AB of length 13 meters, which is leaning against a vertical wall as shown in figure and its base slides away from the wall. At the instant base B is 12 m from the vertical wall, the base B is moving at the rate of 5 m/sec. A man (M) of height 1.5 meter standing at a distance of 15 m from the vertical wall.

The rate at which the length of shadow of man increases, when the base B is 12 m from vertical wall, is
View SolutionA lamp post of length 10 meter placed at the end A of a ladder AB of length 13 meters, which is leaning against a vertical wall as shown in figure and its base slides away from the wall. At the instant base B is 12 m from the vertical wall, the base B is moving at the rate of 5 m/sec. A man (M) of height 1.5 meter standing at a distance of 15 m from the vertical wall.

Rate at which θ decreases, when the base B is 12 m from the vertical wall, is
View SolutionGiven the setup shown in Fig Block A,B and C have masses mA=M and mB=mC=m. The strings are assumed maseless and unstreichable, and the pulleys frictionless .There is no friction between block B and the support table, but there is friction between blocks B and C, denoted by a given coefficient μ

a . In terms the given find (i) the acceleration of block A and B
b. Suppose the system is released from rest with block C near the right end of block B as shown in the above figure. If the the length L of block B is given, what is the speed of block C as it reached the left end of block B ? Tear the size of C as small
c. If the mass of block A is less then some critical value, the blocks will not accelerate when released from rest. Write down as expression for that critical mass.
View Solution
