Let d1 and d2 be the lengths of the perpendiculars drawn from any point of the line 7x−9y+10=0 upon the lines 3x+4y=5 and 12x+5y=7 respectively. Then (A)d1>d2(B)d1=d2(C)d1<d2(D)d1=2d2
7h−9y+10=0
9y=7h+10
y=7h+109
d1=∣∣
∣
∣∣3h+4(7h+109)−5√9+16∣∣
∣
∣∣
d1=∣∣∣27h+28h+40−4545∣∣∣
d1=∣∣∣55h−545∣∣∣
d1=∣∣∣11h−19∣∣∣
d2=∣∣
∣
∣∣12h+5(7h+109)−7√140+25∣∣
∣
∣∣
d2=∣∣∣143h−1313⋅9∣∣∣
d2=∣∣∣11h−19∣∣∣
so, d1−d2.
Similar Questions
If D1andD2 are diagonal matices of order 3×3 then (A) Dn1 is a diagonal matrix (B) D1D2=D2D1 (C) D21+D22 is diagonal matrix (D) D1D2 is a diagonal matix
View SolutionStatement 1: if D=diag[d1,d2,,dn],then D−1=diag[d−11,d−12,...,d−1n] Statement 2: if D=diag[d1,d2,,dn],then Dn=diag[dn1,dn2,...,dnn]
View SolutionA line meets the coordinate axes at A and B . A circle is circumscribed about the triangle O A Bdot If d_1a n dd_2 are distances of the tangents to the circle at the origin O from the points Aa n dB , respectively, then the diameter of the circle is (2d_1+d_2)/2 (b) (d_1+2d_2)/2 d_1+d_2 (d) (d_1d_2)/(d_1+d_2)
View SolutionLet d_1a n dd_2 be the length of the perpendiculars drawn from the foci Sa n dS ' of the ellipse (x^2)/(a^2)+(y^2)/(b^2)=1 to the tangent at any point P on the ellipse. Then, S P : S^(prime)P= (a) d_1: d_2 (b) d_2: d_1 (c) d_1 ^2:d_2 ^2 (d) sqrt(d_1):sqrt(d_2)
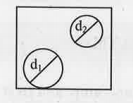
View SolutionThe metal sheet shown in figure, with two holes cut of unequal diameters d1, and d2(d1>d2). If the sheet is heated
View Solutionଦୁଇଟି ଅନ୍ତଃସ୍ପର୍ଶ ବୃତ୍ତର ବ୍ୟାସ d_1 ଓ d_2 ସେ. ମି (d_1>d_2) ସେମାନଙ୍କ କେନ୍ଦ୍ର ମଧ୍ୟରେ ଦୂରତା କେତେ ସେ. ମି ?
View SolutionIf f_1(x) and f_2(x) are defined on domains D_1 and D_2 ,respectively, then f_1 (x) + f_2(x) is defined on D_1 nn D_2 .
View SolutionIf f_1 (x) and f_2 (x) are defined on domains D_1 and D_2 respectively, then f_1 (x) + f_2 (x) is defined on D_1 uu D_2 .
View Solution
