Given R1=5.0±0.2Ω,andR2=10.0±0.1Ω. What is the total resistance in parallel with possible % error?
15Ω±2%
3.3Ω±3%
15Ω±3%
3.3Ω±7%
The correct Answer is:B
Step by step video & image solution for Given R_(1) = 5.0 +- 0.2 Omega, and R_(2) = 10.0 +- 0.1 Omega. What is the total resistance in parallel with possible % error? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
108 . If two resistors of resistances R1=(4±0.5)ΩandR2=(16±0.5)Ω are connected (i) in series and (ii) in parallel, find the equivalent resistance in each case with limits of percentage error.
View Solution1resistances R_(1)=(3.0+-0.1)Omega and R_(2)=(6.0+-0.2)Omega are to be joined together. (A) The maximum resistance obtainable is (9.0+-0.3)Omega (B) The maximum resistance obtainable is (9.0+-0.2)Omega (C) The minimum resistance obtainable is (2.0+-0.3)Omega (D) The minimum resistance obtainable is (2.0+-0.2)Omega
View Solution
Knowledge Check
Given Resistance R1=(8±0.4)Ωand Resistence, R2=(8±0.6)Ω What is the net resistence when R1 and R2 are connected in series?
A(16±0.4Ω)B(3.45±0.3)ΩC(3.45±0.4)ΩD(3.45±0.5)ΩTwo resistor R1=(24±0.5)ΩandR2=(8±0.3)Ωare joined in series, The equivalent resistance is
A32±0.33ΩB32±0.8ΩC32±0.2ΩD32±0.5ΩTwo carbon resistances are given by R1=(4±0.4) ohm and R2=(12±0.6)Ω. What is their net resistance with percentage error, if they are connected in series?
A16Ω±5%B16Ω±6.25%C16Ω±8%D16Ω±12%
In the circuit shown in Fig. the emf of the sources is equal to ξ=5.0V and the resistances are equal to R1=4.0Ω and R2=6.0Ω. The internal resistance of the source equals R=1.10Ω. Find the currents flowing through the resistances R1 and R2.
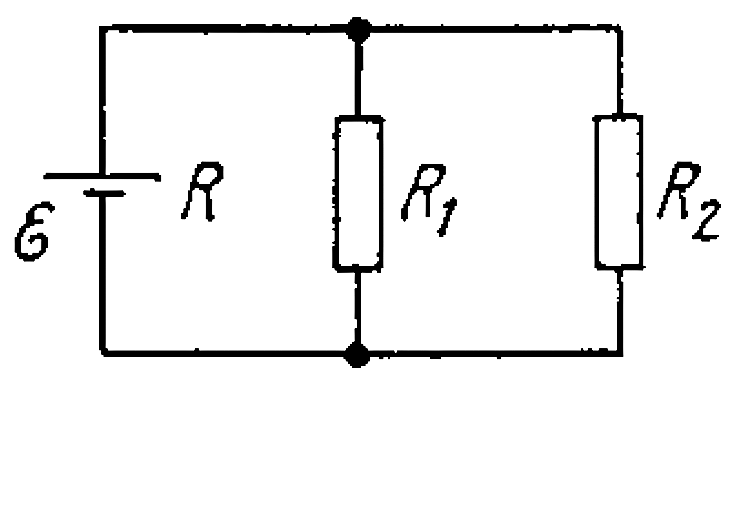
View SolutionThree cells of emf, ε1=1.5V,ε2=2.0Vandε3=3.0V having internal resistance r1=0.30Ω,r2=0.4Ωandr3=0.6Ω respectively are connected in parallel. Find out the equivalent emf and the equivalent resistance of a cell which can replace this combination.
View SolutionTwo resistors R1=(4±0.8)ΩandR2(4±0.4)Ω are connected in parallel. The equivalent resistance of their parallel combination will be :
View SolutionTwo resistor of resistance R1=(6±0.09)Ω and R2=(3±0.09)Ω are connected in parallel the equivalent resistance R with error (in Ω)
View SolutionThe values of two resistors are R1=(6±0.3)kΩ and R2=(10±0.2)kΩ. The percentage error in the equivalent resistance when they are connected in parallel is
View Solution
