A transever sine wave of amplitude 10 cm and wavelength 200 cm travels from left to right along a long horizontal stretched, string is at the origin and is moving downward. Then the equation of the wave will be ( in CGS system )
y=10sin(0.01π×−πt)
y=10sin(πt−0.01π×)
y=10sin(0.02π×−0.01πt)
y=10sin(πt−0.02π×)
The correct Answer is:A
Step by step video, text & image solution for A transever sine wave of amplitude 10 cm and wavelength 200 cm travels from left to right along a long horizontal stretched, string is at the origin and is moving downward. Then the equation of the wave will be ( in CGS system ) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - More Than One Option is Correct23videos
WAVE MOTION
- BOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Comprehion Type Questions19videos
WAVE MOTION
- BOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - JEE MAINS50videos
WAVE MOTION
- BOOK - DC PANDEYCHAPTER - VECTORSEXERCISE - Medical enrances gallery9videos
VECTORS
- BOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based2videos
WORK, ENERGY & POWER
Similar Questions
An harmonic wave has been set up on a very long string which travels along the length of the string. The wave has a frequency of 50 Hz, amplitude 1 cm and wavelength 0.5 m. find
(a) the time taken by the wave to travel a distance of 8 m along the length of string (b) the time taken by a point on the string to travel a distance of 8 m, once the wave has reached the point and sets it into motion (c ) also. consider the above case when the amplitude gets doubledView SolutionTwo sinusoidal waves with the same amplitude and wavelength travel through each other along a string that is stretched along an x axis. Their resultant wave is shown twice in Fig. 16-53, as the antinode A travels from an extreme upward displacement to an extreme downward displacement in 6.0 ms. The tick marks along the axis are separated by 15 cm, height H is 1.20 cm. Let the equation for one of the two waves be of the form y(x,t)=ymsin(kx+ω). In the equation for the other wave, what are (a)ym(b)k,(c)ω, and (d) the sign in front of ω?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The equation of a wave of amplitude 0.02 m and period 0.04 s travelling along a stretched string with a velocity of 25m/s will be
Ay=0.02sin2π(0.04t−0.5x)By=0.02sin2π(25t−2x)Cy=0.02sin2π(0.04t−x)Dy=0.02sin2π(25t−x) - Question 2 - Select One
A transverse sinusoidal wave is generated at one end of a long horizontal string by a bar that moves the end up and down through a distance by 2.0cm. the motion of bar is continuous and is repeated regularly 125 times per second. If klthe distance between adjacent wave crests is observed to be 15.6cm and the wave is moving along positive x−direction, and at t=0 the element of the string at x=0 is at mean position y=0 and is moving downward, the equation of the wave is best described by
Ay=(1cm)sin[(40.3rad/m)x−(786rad/s)t]By=(2cm)sin[(40.3rad/m)x−(786rad/s)t]Cy=(1cm)cos[(40.3rad/m)x−(786rad/s)t]Dy=(2cm)cos[(40.3rad/m)x−(786rad/s)t] - Question 3 - Select One or More
A transverse sinusoidal wave of amplitude a, wavelength λ and frequency f is travelling on a stretched string. The maximum speed of any point in the string is v/10, where v is the speed of propagation if the wave. If a=10−3m and v=10ms−1, then lanbda and f are given by
A(a) λ=2π×10−2mB(b) λ=10−3mC( c ) f=103Hz/(2π)D(d) f=104Hz
A sinusoidal transverse wave of amplitude 10−2 m, wavelength λ, frequency f is travelling with speed (V = 20 m/s) on a stretched string. If the maximum speed at any point of the string is V5 then find the frequency and wavelength of the wave.
View SolutionA sound wave has frequency 5 kHz and wavelength 20cm. How long will it take to travel 2 km?
View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. The transverse displacement of the string particle at as a function of time is shown in Figure.
The equation of the wave with all the constants evaluated is:
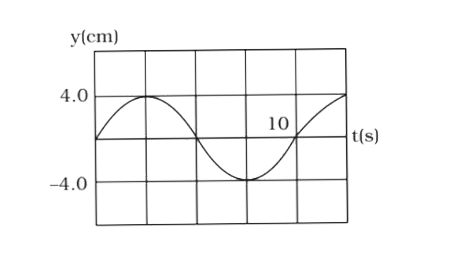 View Solution
View SolutionA transverse wave, whose amplitude is 0.5 m wavelength is 1 m and frequency is 2Hz. is travelling along positive x direction. The equation of this wave will be-
View SolutionA transverse sinusoidal wave of amplitude A, wavelength λ and frequency f is travelling along a stretch string. The maximum speed of any point on the string is v10, where, V is the velocity of wave propagation. If A=10−3m,andV=10ms−1, then λ and f are given by
View Solution

