A person's eye is at a height of 1.5 m . He stands infront of a 0.3 m long plane mirror whose lower end is 0.8m above the ground. The length of the image he sees of himself is
1.5 m
1.0 m
0.8 m
0.6 m
The correct Answer is:D
To solve the problem, we need to determine the length of the image a person sees in a plane mirror. Here’s a step-by-step solution:
Step 1: Understand the setup
- The height of the person's eye from the ground is 1.5 m.
- The height of the lower end of the mirror from the ground is 0.8 m.
- The length of the mirror is 0.3 m.
Step 2: Determine the height of the upper end of the mirror
- Since the lower end of the mirror is at 0.8 m and the mirror is 0.3 m long, the upper end of the mirror is at:
Height of upper end=0.8m+0.3m=1.1m
Step 3: Analyze the image formation
- In a plane mirror, the image formed is of the same height as the object and appears at the same distance behind the mirror as the object is in front of it.
- The image of the person's eye will be located at a height equal to the height of the eye above the ground, which is 1.5 m.
Step 4: Determine the effective height for the image
- The person's eye is at 1.5 m, and since the mirror's upper end is at 1.1 m, the image will be reflected from the mirror.
- The distance from the person's eye (1.5 m) to the upper end of the mirror (1.1 m) is:
Distance from eye to upper end of mirror=1.5m−1.1m=0.4m
- The image will appear at the same height as the person's eye, which is 1.5 m, but since the mirror only goes up to 1.1 m, we need to consider the height of the image that can be seen in the mirror.
Step 5: Determine the visible height of the image
- The height of the image that can be seen in the mirror is limited by the height of the mirror. Since the mirror is 0.3 m long and starts at 0.8 m, it can reflect the image from 0.8 m to 1.1 m.
- The height of the image seen in the mirror will be:
Height of image=Height of eye−Height of lower end of mirror=1.5m−0.8m=0.7m
Step 6: Conclusion
- Therefore, the length of the image that the person sees of himself in the mirror is:
Length of the image=0.3m
Final Answer
The length of the image he sees of himself is 0.3 m.
---
- The height of the person's eye from the ground is 1.5 m.
- The height of the lower end of the mirror from the ground is 0.8 m.
- The length of the mirror is 0.3 m.
- Since the lower end of the mirror is at 0.8 m and the mirror is 0.3 m long, the upper end of the mirror is at:
Height of upper end=0.8m+0.3m=1.1m
- In a plane mirror, the image formed is of the same height as the object and appears at the same distance behind the mirror as the object is in front of it.
- The image of the person's eye will be located at a height equal to the height of the eye above the ground, which is 1.5 m.
- The person's eye is at 1.5 m, and since the mirror's upper end is at 1.1 m, the image will be reflected from the mirror.
- The distance from the person's eye (1.5 m) to the upper end of the mirror (1.1 m) is:
Distance from eye to upper end of mirror=1.5m−1.1m=0.4m
- The image will appear at the same height as the person's eye, which is 1.5 m, but since the mirror only goes up to 1.1 m, we need to consider the height of the image that can be seen in the mirror.
- The height of the image that can be seen in the mirror is limited by the height of the mirror. Since the mirror is 0.3 m long and starts at 0.8 m, it can reflect the image from 0.8 m to 1.1 m.
- The height of the image seen in the mirror will be:
Height of image=Height of eye−Height of lower end of mirror=1.5m−0.8m=0.7m
- Therefore, the length of the image that the person sees of himself in the mirror is:
Length of the image=0.3m
The length of the image he sees of himself is 0.3 m.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - A. Only one option is correct (JEE Advance)
73 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - B. More than one option is correct
20 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
Similar Questions
A person's eye is at a height of 1.5m.He stands in frount of a 0.3 m length palne mirror bottom of which is 0.8 m above ground.Find the length the of his image he will be able in this mirror
[0.6 m]
View SolutionA balloon is moving upwards with a speed of 20m/s. When it is at a height of 14 m from ground in front of a plane mirror in situation as shown in figure, a boy drops himself from the balloon. Find the time duration for which he will see the image of source S placed symmetrically before plane mirror during free fall.
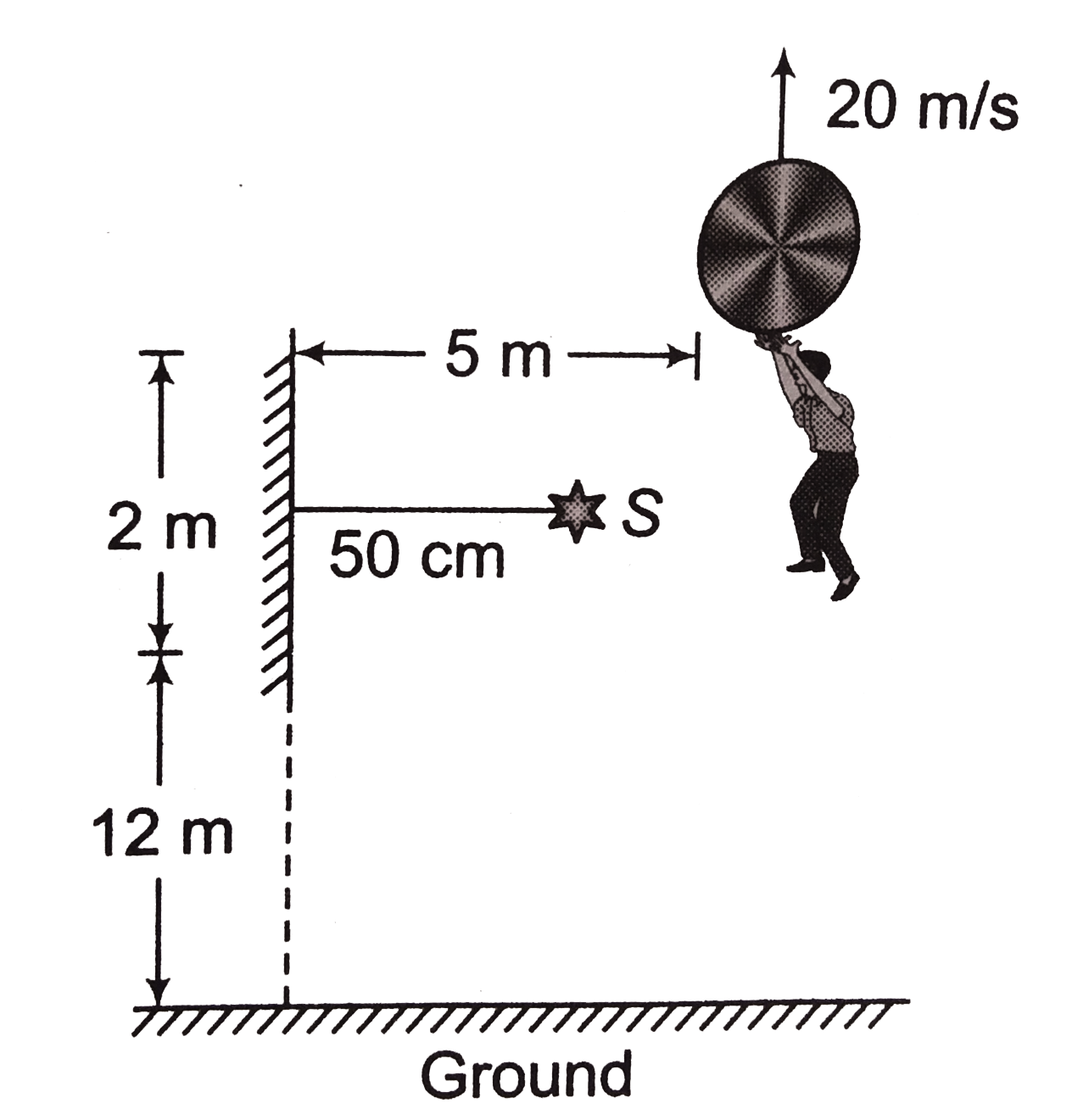
View Solution
Knowledge Check
A person's eye is at a height of 1.5m. He stands infront of a 0.3m long palane mirror which is 0.8m above the ground. The length of the image he sees of himself is:
A1.5mB1.0mC0.8mD0.6mA boy whose eyes are 150 cm above the ground looks at his reflection in a vertical mirror 200 cm away. The top and bottom of the mirror are 220 cm and 120 cm above the ground respectively. What length below his eyes can he see, of himself in the mirror?
A60 cmB75 cmC100 cmD120 cmA boy of height 1m stands in front of a convex mirror. His distance from the mirror is equal to its focal length. The height of his image is
A0.25mB0.33mC0.5mD0.67m
Ramesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it) (see the figure). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively.
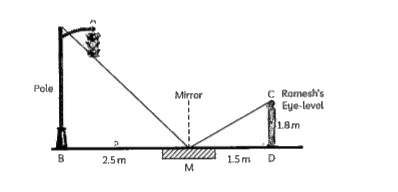
If Ramesh's eye level is 1.2 m above the ground, then the height of the pole is:
View SolutionA body of height 1m stands in front of a convex mirro. His distance from the mirror is equal to its focal length. The height of his image is
View SolutionA person AB of height 170 cm is standing in front of a plane mirror. His eyes are at height 164 cm. At what distance from P should a hole be made in mirror so that he cannot see his hair?

View SolutionA man 160 cm height stands in fromt of a plane mirror . His eyes are at a height of 150 cm from the floor. Then the minimum length of the plane mirror for him to see his full length image is -
View SolutionA pole of height 1 . 8 m stands in front of a larger vertical plane mirror . The distance of the image from the pole at a distance of 1 . 5 m from the mirror is
View Solution
