For an equilateral prism, it is observed that when a ray strikes grazingly at one face it emerges grazingly at the other. Its refractive index will be
√3
2√3
2
Data not sufficient
The correct Answer is:C
To find the refractive index of an equilateral prism when a ray strikes grazingly at one face and emerges grazingly at the other, we can follow these steps:
1. Understand the Geometry of the Prism:
- An equilateral prism has an angle of A=60∘.
2. Identify the Incident and Emergent Angles:
- When a ray strikes the prism grazingly, the angle of incidence i at the first face is 90∘.
- Since it emerges grazingly at the other face, the angle of emergence e is also 90∘.
3. Apply Snell's Law at the First Face:
- According to Snell's Law:
n1sini=n2sinr1
- Here, n1=1 (the refractive index of air), i=90∘, and r1 is the angle of refraction at the first face.
- Since sin90∘=1, we have:
1⋅1=nsinr1⟹n=sinr1
4. Apply Snell's Law at the Second Face:
- At the second face, we apply Snell's Law again:
nsinr2=1⋅sine
- Here, e=90∘, so:
nsinr2=1⋅1⟹n=1sinr2
5. Use the Prism Property:
- For a prism, the sum of the angles of refraction at both faces is equal to the angle of the prism:
r1+r2=A
- Since A=60∘, we have:
r1+r2=60∘
6. Since r1=r2:
- Let r1=r2=r. Therefore:
r+r=60∘⟹2r=60∘⟹r=30∘
7. Calculate the Refractive Index:
- From the earlier equations, we can substitute r:
n=sinr1=sin30∘=12
- Thus, the refractive index n is:
n=2
Final Answer:
The refractive index of the equilateral prism is n=2.
- An equilateral prism has an angle of A=60∘.
- When a ray strikes the prism grazingly, the angle of incidence i at the first face is 90∘.
- Since it emerges grazingly at the other face, the angle of emergence e is also 90∘.
- According to Snell's Law:
n1sini=n2sinr1
- Here, n1=1 (the refractive index of air), i=90∘, and r1 is the angle of refraction at the first face.
- Since sin90∘=1, we have:
1⋅1=nsinr1⟹n=sinr1
- At the second face, we apply Snell's Law again:
nsinr2=1⋅sine
- Here, e=90∘, so:
nsinr2=1⋅1⟹n=1sinr2
- For a prism, the sum of the angles of refraction at both faces is equal to the angle of the prism:
r1+r2=A
- Since A=60∘, we have:
r1+r2=60∘
- Let r1=r2=r. Therefore:
r+r=60∘⟹2r=60∘⟹r=30∘
- From the earlier equations, we can substitute r:
n=sinr1=sin30∘=12
- Thus, the refractive index n is:
n=2
The refractive index of the equilateral prism is n=2.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - B. More than one option is correct
20 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - C. comprehension type question
14 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
Similar Questions
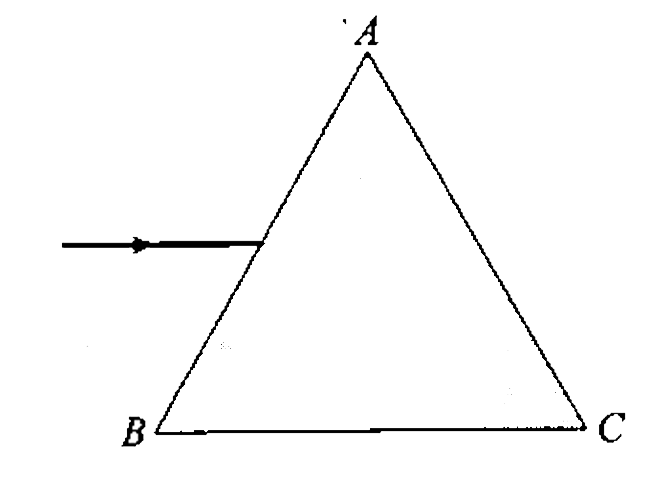
A ray of light is incident on an equilateral triangular prism parallel to its base as shown in the figure. The ray just fails to emerge from the face AC. If μ be the refractive index of the prism then the relation(s) is/are :
View SolutionA ray of light is incident at an angle of 60° on one face of a 30∘) prism. The emergent ray from the prism makes an angle of 30∘ with the incident ray. Show that the emergent ray is normal to the surface from which it emerges. Calculate the refractive index of the material of the prism.

View Solution
Knowledge Check
For an equilateral prism, it is observed that when a ray strikes grazingly at one face, it emerges grazingly at the other face, its refractive index will be
A√32B2√3C2D43There is a equilateral prism of refractive index 3 on which a light ray is incident normally on one face as shown in the figure. Find the length of the path traveled by the light ray inside the prism.
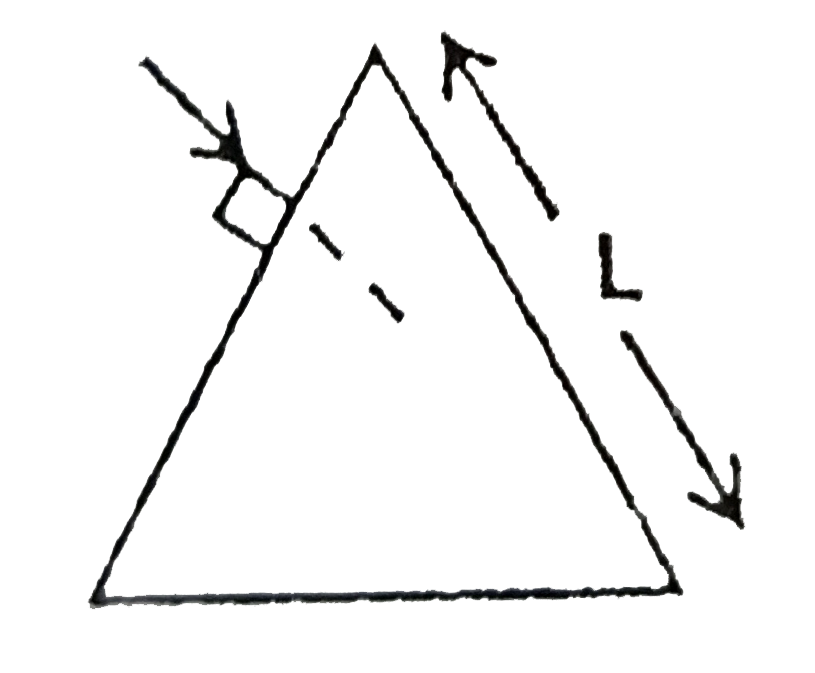 A√3L2B√3LC3L/2DL
A√3L2B√3LC3L/2DL
A ray of light is incident at an angle of 60∘ on the face of a prism having refracting angle 30∘. The ray emerging out of the prism makes an angle 30∘ with the incident ray. Show that the emergent ray is perpendicular to the face through which it emerges and calculate the refractive index of the material of prism.
View SolutionOn one face of an equilateral prism a light rays strikes normally. If its μ=32, find the angle between incident ray and the ray that leaves the prism.
[60∘]
View SolutionIn an isosceles prism of prism angle 45∘, it is found that when the angle of incidence is same as the prism angle, the emergent ray grazes the emergent surface. Find the refractive index of the material of the prism.For what angle of incidence the angle of deviation will be minimum ?
View SolutionA ray of light is incident horizontally on the face AB of the.right angled prism as shown in the figure. If the ray emerges grazing the surface AC, find the value of ϕ. Refractive index of the material of the prism is given to be n.
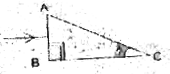
View SolutionA ray of light passes through an equilateral prism in such a way that the angle of incidence is equal to the angle of emergence and each of these angles is 3/4th the angle of the prism. Determine the (i) angle of deviation and (ii) the refractive index of the prism.
View SolutionA ray of light passes through an equilateral glass prism in such a way that the angle of incidence is equal to the angle of emergence and each of these angles is 34 times the angle of the prism. Determine the angle of deviation and the refractive index of the glass prism.
View Solution
