A convex lens of focal length 10 cm is painted black at the middle portion as shown in figure. An object placed at a distance of 20 cm from the lens. Then
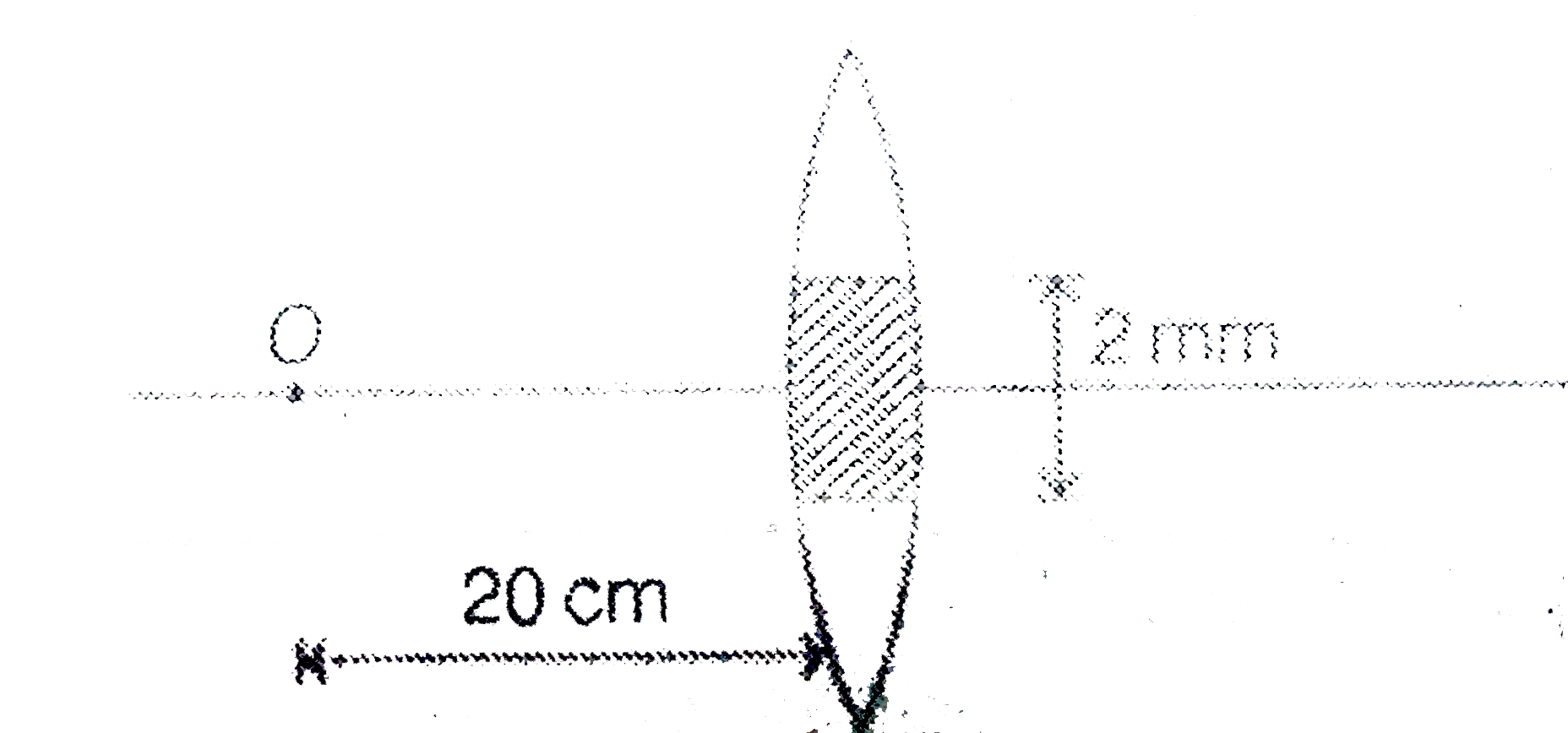
only one image will be formed by the lens
the distance between the two images formed by such a lens is 6 mm
the distance between the images is 4 mm
the distance between the images is 2mm
The correct Answer is:A
Step by step video, text & image solution for A convex lens of focal length 10 cm is painted black at the middle portion as shown in figure. An object placed at a distance of 20 cm from the lens. Then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - B. More than one option is correct20videos
RAY OPTICS
- BOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - C. comprehension type question14videos
RAY OPTICS
- BOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.15videos
RAY OPTICS
- BOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer8videos
PROPERTIES OF MATTER
- BOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
Similar Questions
One half of a convex lens of focal length 10 cm is covered with a black paper. Can such a lens produce an image of a complete object placed at a distance of 30 cm from the lens? Draw a ray diagram to justify your answer.
A4 cm tall object is placed perpendicular to the principal axis of a convex lens of focal length 20 cm. The distance of the object from the lens is 15 cm. Find the nature, position and size of the image.View SolutionA needle 10 cm long is placed along the axis of a convex lens of focal length 10 cm such that the middle point of the neddle is at a distance of 10 cm from the lens. Find the length of the image of the neddle.
View Solution
Knowledge Check
- Question 1 - Select One
A convex lens of focal length 10cm is painted black at the middle portion as shown in figure . An object is placed at a distance 20cm from the lens. Then,
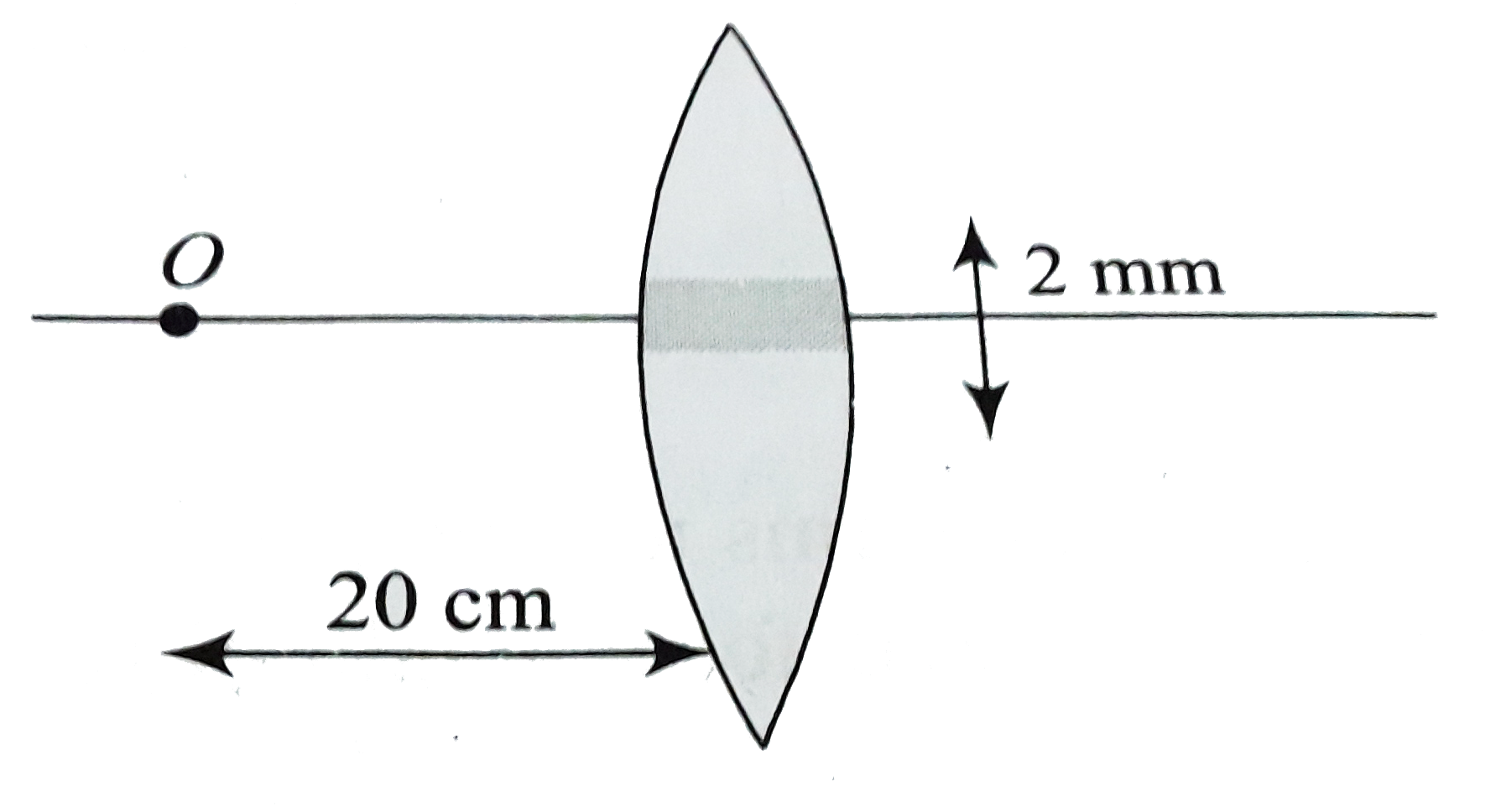Aonly one image will be formed by the lensBthe distance between the two images formed by such a lens is 6mmCthe distance between the images is 4mmDthe distance between the images is 2mm - Question 2 - Select One
A convex lens of focal length 30 cm , a concave lens of focal length 120 cm , and a plane mirror are arranged as shown . For an object kept at a distance of 60 cm from the convex lens, the final image, formed by the combination , is a real image , at a distance of :
_E01_195_Q01.png)
|Focal length|=|Focal length|
= 30cm =120cm
_S01_267_Q02.png)
A70 cm from the convex lensB60 cm from the convex lensC60 cm from the concave lensD70 cm from the concave lens - Question 3 - Select One
A point object is placed at a distance of 12cm from a convex lens of focal length 10cm. On the other side of the lens, a convex mirror is placed at a distance of 10cm from the lens such that the image formed by the combination coincides with the object itself. The focal length of the convex mirror is
A20cmB25cmC15cmD30cm
One half of a convex lens of focal length 10 cm is covered with a black paper. Can such
a lens produce an image of a complete object placed at a distance of 30 cm from the
lens? Draw a ray diagram to justify your answer. A 4 can tall object is placed
perpendicular to the perpendicular to the principal axis of a convex lens of focal length 20 cm. The distince
of the object from the less is 15 cm. Find nature, position and size of the image.View SolutionAn object is placed at a distance of 30 cm from a convex lens of focal length 20 cm.
View SolutionWhat is the position of image when an object is placed is at a distance of 10 cm from a convex lens of focal length 10 cm?
View SolutionA convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
View SolutionA convex lens of focal length 20 cm and a concave lens of focal length 10 cm are placed 20 cm apart. In between them an object placed at distance x from the convex lens.
What will be the linear magnification produced convex lens and concave lens individually ?View Solution