Question

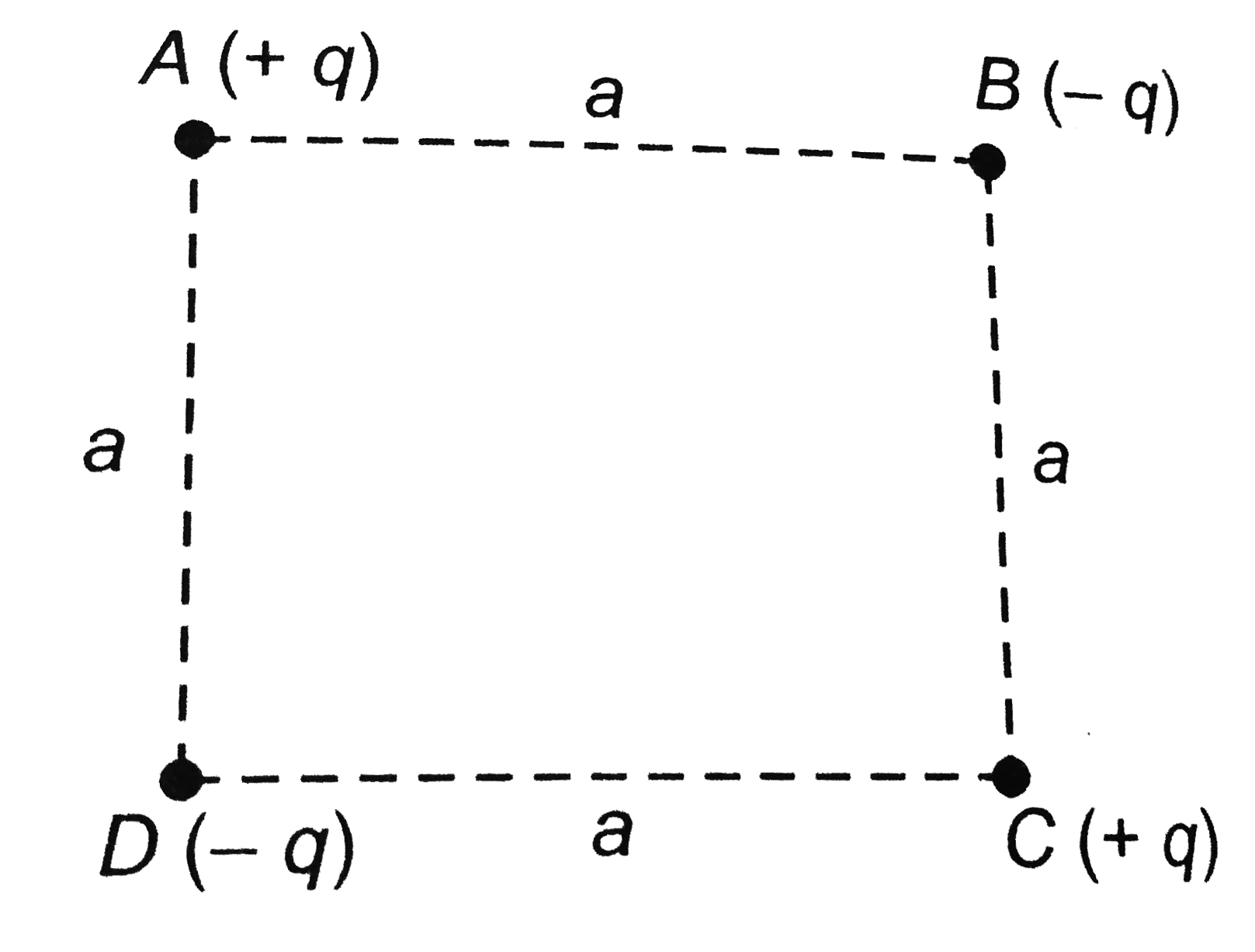
Four point charge $q,-q,2Q$ and Q are placed in order at the corners A, B, C and D of a square. If the field at the midpoint of CD is zero then the value of $q/Q$ is $\frac{5\sqrt{5}}{x}$. Find the value of x.

Answer

2

Explanation

To solve the problem, we need to analyze the electric field at the midpoint of line segment CD in the square formed by the charges. Let's denote the corners of the square as follows:

- A (top left corner) has charge $$q$$
- B (top right corner) has charge $$-q$$
- C (bottom right corner) has charge $$2Q$$
- D (bottom left corner) has charge $$Q$$

Step 1: Identify the Midpoint of CD
The midpoint \( M \) of line segment \( CD \) can be expressed in terms of coordinates. If we assume the square has a side length \( a \), the coordinates of the corners are:
- C: \( (a, 0) \)
- D: \( (0, 0) \)

Thus, the coordinates of midpoint \( M \) are:
\( M = \left( \frac{a}{2}, 0 \right) \)

Step 2: Calculate the Electric Field at M due to Each Charge
The electric field \( \vec{E} \) due to a point charge \( q \) at a distance \( r \) is given by:
\( \vec{E} = \frac{k \cdot q}{r^2} \hat{r} \)
where \( k \) is Coulomb's constant and \( \hat{r} \) is the unit vector pointing away from the charge.

Electric Field due to Charge at A (q):
- Distance from A to M: \( \frac{a}{\sqrt{2}} \)
- Direction: towards the right (positive x-direction)
\( E_A = \frac{k \cdot q}{\left(\frac{a}{\sqrt{2}}\right)^2} = \frac{2kq}{a^2} \)

Electric Field due to Charge at B (-q):
- Distance from B to M: \( \frac{a}{2} \)
- Direction: towards the left (negative x-direction)
\( E_B = -\frac{k \cdot (-q)}{\left(\frac{a}{2}\right)^2} = \frac{4kq}{a^2} \)

Electric Field due to Charge at C (2Q):
- Distance from C to M: \( \frac{a}{2} \)
- Direction: towards the left (negative x-direction)
\( E_C = -\frac{k \cdot (2Q)}{\left(\frac{a}{2}\right)^2} = -\frac{8kQ}{a^2} \)

Electric Field due to Charge at D (Q):
- Distance from D to M: \( \frac{a}{2} \)
- Direction: towards the right (positive x-direction)
\( E_D = \frac{k \cdot Q}{\left(\frac{a}{2}\right)^2} = \frac{4kQ}{a^2} \)

Step 3: Set Up the Equation for Zero Electric Field
For the electric field at point M to be zero, the sum of the electric fields due to all charges must equal zero:
\( E_A + E_B + E_C + E_D = 0 \)
Substituting the expressions we found:
\( \frac{2kq}{a^2} + \frac{4kq}{a^2} - \frac{8kQ}{a^2} + \frac{4kQ}{a^2} = 0 \)
This simplifies to:
\( 6q - 4Q = 0 \)
Thus:
\( 6q = 4Q \implies \frac{q}{Q} = \frac{4}{6} = \frac{2}{3} \)

Step 4: Relate to Given Ratio
According to the problem, we have:
\( \frac{q}{Q} = \frac{5\sqrt{5}}{x} \)
Setting the two ratios equal gives:
\( \frac{2}{3} = \frac{5\sqrt{5}}{x} \)
Cross-multiplying yields:
\( 2x = 15\sqrt{5} \implies x = \frac{15\sqrt{5}}{2} \)

Final Answer
Thus, the value of \( x \) is:
\( \boxed{\frac{15\sqrt{5}}{2}} \)