Two sheets of thickness d and 2d and same area are touching each other on their face. Temperature TA,TB,TC shown are in geometric progression with common ratio r = 2. Then ratio of thermal conductivity of thinner and thicker sheet are
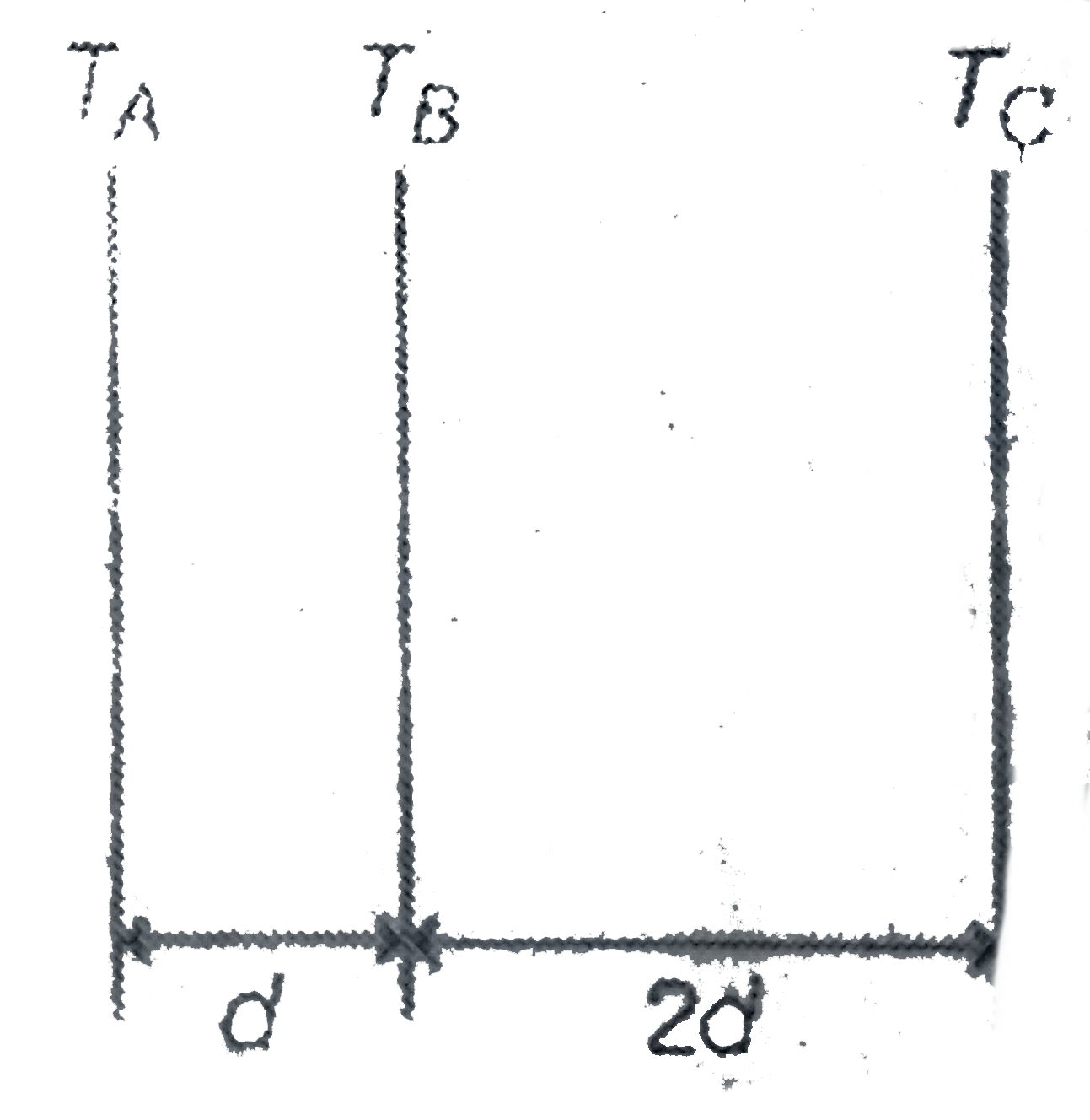
1
2
0.5
4
The correct Answer is:A
Step by step video, text & image solution for Two sheets of thickness d and 2d and same area are touching each other on their face. Temperature T_(A),T_(B),T_(C) shown are in geometric progression with common ratio r = 2. Then ratio of thermal conductivity of thinner and thicker sheet are by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
If a,b,c are the first three non-zero terms of a geometric progression such that a−2,2band12c forms another geometric progression with common ratio 5, then the sum of the series a+b+c+...+∞, is
View SolutionIf a,b,c are the first three non-zero terms of a geometric progression such that a=2,2b and 12c forms another geometric progression with common ratio 5, then the sum of the series a+b+c+..∞, is.
View Solution
Knowledge Check
- Question 1 - Select One
Two sheets of thickness d and 3d and of same area are joined together. Temperature TA,TB,TC shown in the figure are in geometric progression with common ration r=3. Then ratio of thermal conductivity of thinner to thicker sheet is
 A1B2C3D4
A1B2C3D4 - Question 2 - Select One
Two sheets of thickness d and 3d, are touching each other. The temperature just outside the thinner sheet is T1 and on the side of the thicker sheet is T3. The interface temperature is T2.T1,T2andT3 are in arithmetic progression. The ratio of thermal conductivity of thinner sheet to thicker sheet is
A1:3B3:1C2:3D3:9 - Question 3 - Select One
If a,b,c are in geometric progression and a,2b,3c are in arithmetic progression, then what is the common ratio r such that 0<r<1 ?
A13B12C14D18
Find the heat current through the frustum of a cone shown in figure-4.20. Temperature of its two ends are maintained at T1 and T2(T_(2)>T_(1)) respectively and the thermal conductivity of the material is k.
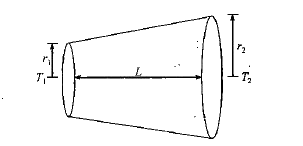 View Solution
View SolutionLet n≥3 and let C1,C2,....,Cn, be circles with radii r1,r2,...rn, respectively. Assume that Ci and Ci+1 touch externally for 1≤i≤n−1. It is also given that the x-axis and the line y=2√2x+10 are tangential to each of the circle . Then r1,r2.rn are in (A) an arithmetic progression with common difference 3+√2 (B) a geometric progression with common ratio 3+√2 (C) an arithmetic progression with common difference 2+√3 (D) a geometric progression with common ratio 2+√3
View SolutionThree rods of the same length and the same area of the cross-section are joined. The temperature of two ends one T1 and T2 as shown in the figure.
 As we move along the rod the variation of temperature are as shown in the following [Rods are insulated from the surrounding except at the faces]
As we move along the rod the variation of temperature are as shown in the following [Rods are insulated from the surrounding except at the faces]
 View Solution
View SolutionTwo walls of thickness d and d and thermal conductivities k and k are in contact. In the steady state, if the temperature at the outer T1 and T2 , the temperature at the common wall is
View SolutionTwo rods of length d1 and d2 and coefficients of thermal conductivites K1 and K2 are kept touching each other. Both have the same area of cross-section. The equivalent thermal conductivity.
View Solution

