A certain amount of ideal monoatomic gas undergoes a process given by TV1/2= constant. The molar specific heat of the gas for the process will be given by
R/2
−3R/2
3R/2
−R/2
The correct Answer is:D
To find the molar specific heat of the gas for the process defined by TV1/2=constant, we can follow these steps:
Step 1: Rewrite the given equation
The process can be expressed as:
TV1/2=k(where k is a constant)
Step 2: Express temperature in terms of pressure and volume
Using the ideal gas law, we know:
PV=nRT⟹T=PVnR
Substituting this into the equation gives:
PVnRV1/2=k
This simplifies to:
PV3/2nR=k
Thus, we can write:
PV3/2=constant
Step 3: Identify the polytropic process
From the equation PV3/2=constant, we can identify that this is a polytropic process with:
n=32
Step 4: Apply the first law of thermodynamics
The first law of thermodynamics states:
ΔQ=ΔU+ΔW
For a polytropic process, we can express the heat added as:
ΔQ=nCΔT
Where C is the molar specific heat for the process.
Step 5: Calculate the change in internal energy
The change in internal energy for an ideal gas is given by:
ΔU=nCVΔT
For a monoatomic gas, the molar specific heat at constant volume CV is:
CV=32R
Step 6: Calculate the work done
The work done in a polytropic process is given by:
ΔW=nR1−nΔT
Substituting n=32:
ΔW=nR1−32ΔT=nR−12ΔT=−2nRΔT
Step 7: Substitute into the first law equation
Now substituting ΔU and ΔW into the first law:
nCΔT=nCVΔT−2nRΔT
Dividing through by nΔT (assuming ΔT≠0):
C=CV−2R
Step 8: Substitute CV
Substituting CV=32R:
C=32R−2R=32R−42R=−12R
Conclusion
Thus, the molar specific heat of the gas for the process is:
C=−12R
The process can be expressed as:
TV1/2=k(where k is a constant)
Using the ideal gas law, we know:
PV=nRT⟹T=PVnR
Substituting this into the equation gives:
PVnRV1/2=k
This simplifies to:
PV3/2nR=k
Thus, we can write:
PV3/2=constant
From the equation PV3/2=constant, we can identify that this is a polytropic process with:
n=32
The first law of thermodynamics states:
ΔQ=ΔU+ΔW
For a polytropic process, we can express the heat added as:
ΔQ=nCΔT
Where C is the molar specific heat for the process.
The change in internal energy for an ideal gas is given by:
ΔU=nCVΔT
For a monoatomic gas, the molar specific heat at constant volume CV is:
CV=32R
The work done in a polytropic process is given by:
ΔW=nR1−nΔT
Substituting n=32:
ΔW=nR1−32ΔT=nR−12ΔT=−2nRΔT
Now substituting ΔU and ΔW into the first law:
nCΔT=nCVΔT−2nRΔT
Dividing through by nΔT (assuming ΔT≠0):
C=CV−2R
Substituting CV=32R:
C=32R−2R=32R−42R=−12R
Thus, the molar specific heat of the gas for the process is:
C=−12R
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
An ideal monatomic gas undergoes process PV1.25 = constant .Then
Aupon increase in pressure temperature decreasesBupon increase in pressure heat is absorbed by gasCif heat is given to gas its internal energy increasesDheat is absorbed by gas if volume increases - Question 2 - Select One
The specific heat of a gas in a polytropic process is given by-
ARγ−1+RN−1BR1−γ+R1−NCRγ−1−RN−1DR1−γ−R1−N - Question 3 - Select One
One mole of an ideal monoatomic gas undergoes a process as shown in the figure. Find the molar specific heat of the gas in the process.
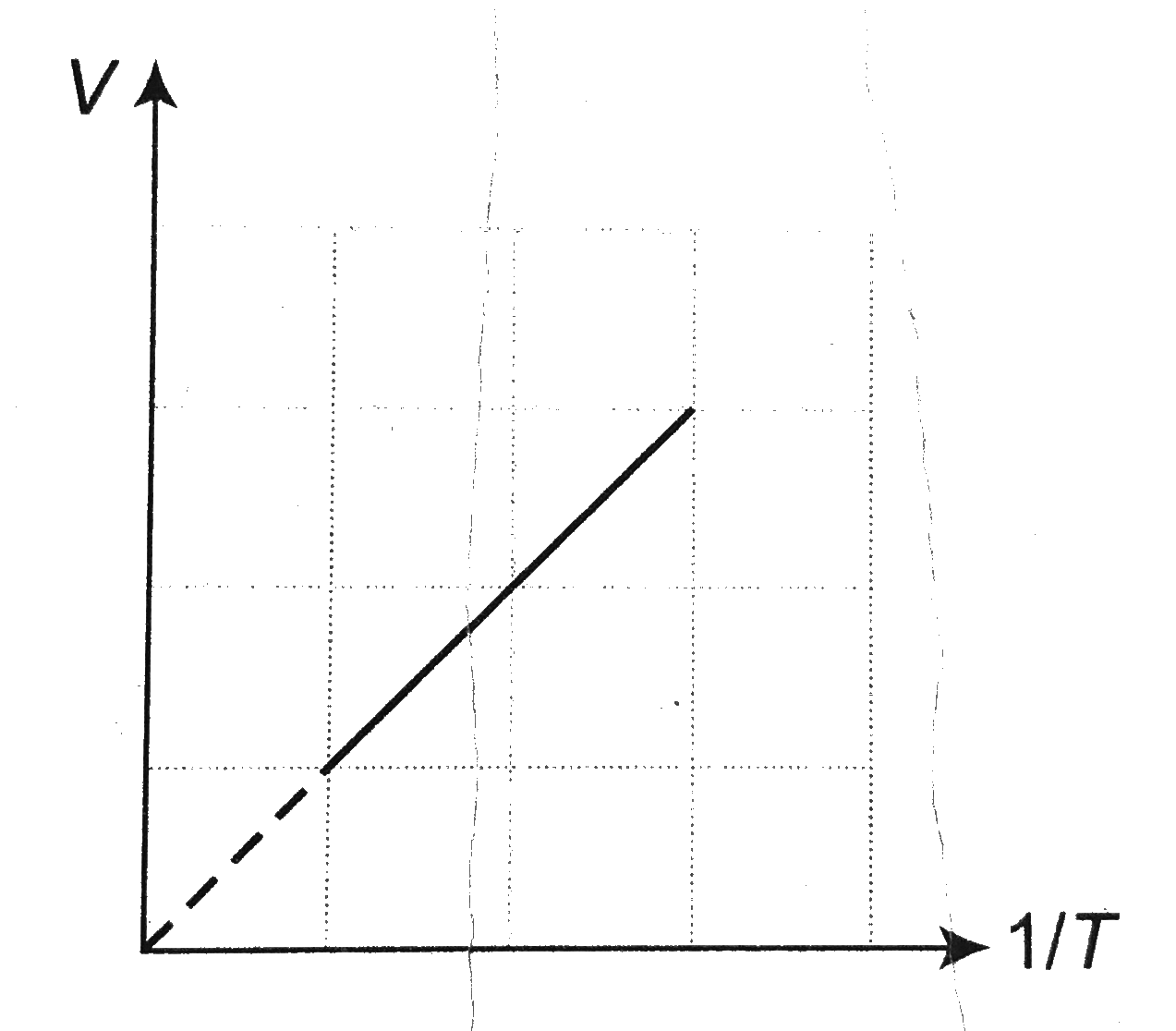
R is a gas constant.A3R4BR2CR3D2R3
One mole of an ideal monoatomic gas undergoes a described by the equations PV3= constant The heat the gas during this process is :
View SolutionTempareture and volume of one mole of an ideal momatomic gas in a process are related as TV23=K ,where k is constant.The molar specific heat capacity for the process is
View SolutionOne mole of a monoatomic ideal gas undergoes process AB in given P – V diagram then average specific heat for this process is:
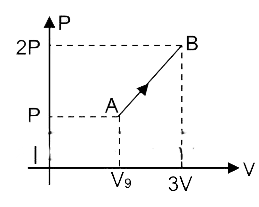 View Solution
View SolutionA certain amount of an ideal monoatomic gas undergoes a thermodynamic process such that VT2= constat where V= volume of gas, T= temperature of gas. Then under process
View SolutionOne mole of a monoatomic ideal gas is expanded by a process described by PV3 = C where C is a constant. The heat capacity of the gas during the process is given by (R is the gas constant)
View Solution

