Somehow Mario gets out of the tunnel and then finds himself face-to-face with the evil gorilla Donkey Kong. Looking down, he saw that he was standing on a gigantic chess- board. He could see various chessmen standing along the board. Donkey Kong shouted, “Domination, total domination! Three challenges, and I want domination in them all!”
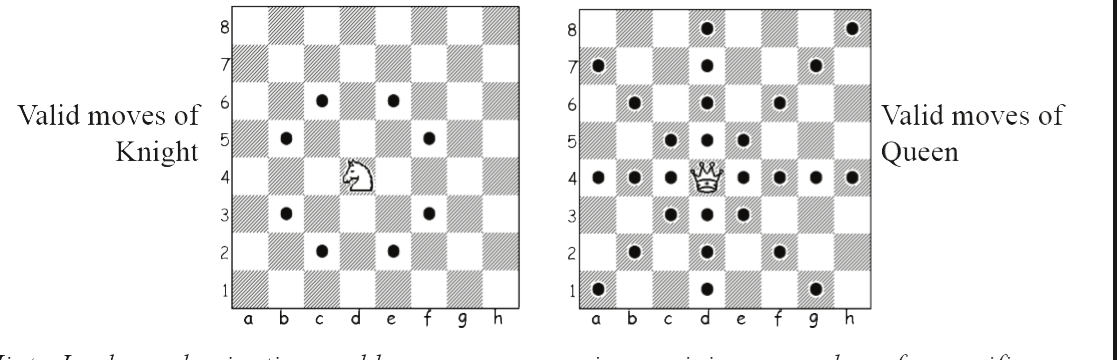
Hint : In chess, domination problems mean arranging a minimum number of a specific type of chess piece such that all places on the board are attacked by atleast one peice.
Total Domination: This is the same as domination but the spaces occupied by the attacking pieces should also be attacked by some other piece.
How many ways can you arrange 4 queens such that they will dominate a 5*9 chess board?
A
4
B
2
C
6
D
None of these
Text Solution
Arrange a queen in 4 of the 5 rows available preferably adjacent ones. So this leaves us with the last row unoccupied by queen. We have now successfully dominated 4 out of the 5 rows. Now, the positions of the queens determine the domination of the last row. Also, the row left unoccupied by queens can be changed to any of the remaining 4 rows which increase the number of solutions. On successfully trying out the different cases out, the number of cases of arrangement of queens to dominate the board turn out to be more than 6.
|
Similar Questions
Knowledge Check
Somehow Mario gets out of the tunnel and then finds himself face-to-face with the evil gorilla Donkey Kong. Looking down, he saw that he was standing on a gigantic chess- board. He could see various chessmen standing along the board. Donkey Kong shouted, “Domination, total domination! Three challenges, and I want domination in them all!”
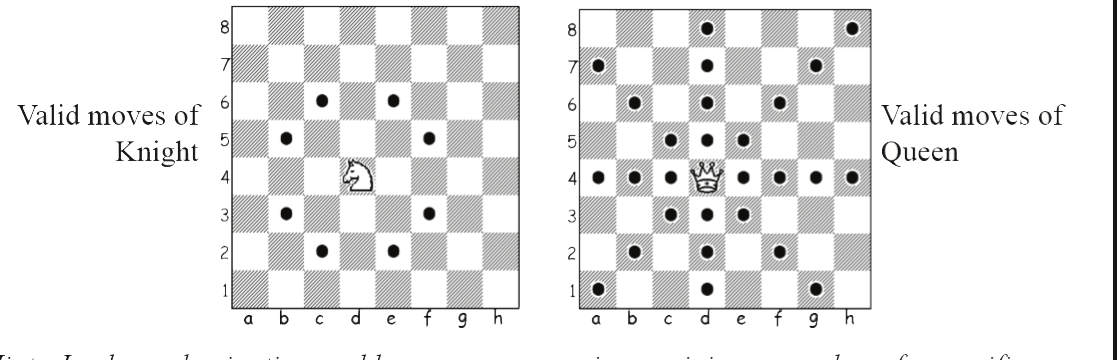
Hint : In chess, domination problems mean arranging a minimum number of a specific type of chess piece such that all places on the board are attacked by atleast one peice.
Total Domination: This is the same as domination but the spaces occupied by the attacking pieces should also be attacked by some other piece.
A 8x8 chess board is in the shape of a torus, where the chess board is on the outer surface of the torus(as shown below). How many minimum number of Knights are required to totally dominate it?
 A8B10C12DNone of these
A8B10C12DNone of theseSomehow Mario gets out of the tunnel and then finds himself face-to-face with the evil gorilla Donkey Kong. Looking down, he saw that he was standing on a gigantic chess- board. He could see various chessmen standing along the board. Donkey Kong shouted, “Domination, total domination! Three challenges, and I want domination in them all!”
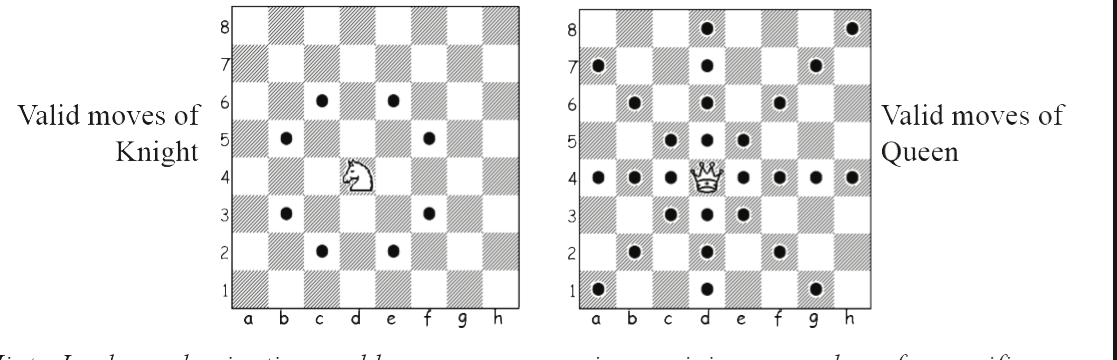
Hint : In chess, domination problems mean arranging a minimum number of a specific type of chess piece such that all places on the board are attacked by atleast one peice.
Total Domination: This is the same as domination but the spaces occupied by the attacking pieces should also be attacked by some other piece.

What are the minimum number of moves knights have to make on the given 8⋅6 chess board so that in their final position, they dominate the entire chessboard if the initial position is as given in the figure beside?A8B10C12DNone of theseThe number of squares that we can find on a chess board is
A64B160C224D204
The number of squares that can be formed on a chess board is
View SolutionConsider a 6 × 6 chess board then the no of rectangles is
View SolutionWhere does the traveller find himself? What problem does he face?
View SolutionApical dominance in plants means
View SolutionWhat does a dominant character mean ?
View Solution
