Further ahead in the market, Mario finds a huge bag containing 171 mushrooms. He reads the label - “Weighing from 1 to 171 kgs, all varieties within”. Mario is puzzled as he does not know which mushrooms weighs what. He goes to a stone seller who had an offer of “Buy 1, Get 2 Identical Stones Free”. Mario asks him for the different kinds of stones and tells that he can use these to measure any of the mushroom accurately(using common balance). How many different kinds of stones does he buy? (Minimum )
“Buy 1, Get 2 Identical Stones Free” means we can have 3 units of every kind of stone we buy.
Answer is 3. We can measure weight of any randomly given mushroom using 3 stones of weights 1 kg ,7 kg & 49 kg (70,71,72 resp.) Suppose we could place stones only in the right pan while a mushroom is in left pan of the balance.
Say we have stones of weight S1= 1kg ,S2= 2kg & S3= 4kg to balance a mushroom M of weight 6,then only S2 & S3 are required to balance M. We can represent above statement using 0 & 1 as the coefficients of S1, S2 & S3. M (on left pan) = 1 x S3 + 1 x S2 + 0 x S1 (on right pan) Note that 110 is also the binary conversion of 7 i.e. we represent 7 in terms of powers of 2 : 1x22+1x21+0x20=7. This way we can measure ANY weight from 1 to 7kg. For range of 171kg, we would require 8 types of weights (i.e. 1, 2,22...upto 27). But there is a shorter way We can instead represent the numbers in powers of 3. Here the coefficients will be 0, 1 or 2. This can do as we have 3 identical copies of each stone. for eg, 16 = 1x9 + 2x3 + 1x1. Giving 121 as the representation. For 171kg, this would require 5 types (1,3,9,27 & 81). If we increase to powers of 4, we require 1,4,16 & 64. (4 kinds) To reach lesser kinds, we’d use powers of 5, coefficients will be 0,1,2,3,4. But we don’t have 4 copies of the stones. But still we can overcome this problem
Now, in the actual question, we can put stones on both sides of the balance. To represent this, we use ‘1’ to denote that a stone is in the left pan, ‘2’ to denote 2 stones in left pan and so on.
for eg,
16 = 1x9 + 2x3 + 1x1
= 1x9 + (31)x3 + 1x1
= 2x9 + (1)x3 + 1x1
In this way, we are putting 3kg on left pan making the weight 19kg on left. Also on right side, weight is 2x9+1x1= 19kg.
The advantage of using both sides is that we can do with only 3 identical copies of each stone, rather than 6. Which means we can use powers of 7 to write the weights. For eg, writing 48 in powers of 7 is 48 = 6x71 + 6x70 (Whenever coefficient crosses 3, convert it to ve number.)
= (71)x7^(1) + (71)x7^(0)
= 1x72 + (1)x71 +1x71+ (1)x70
=1x72 + 1 x 70
So we weigh 48kg by putting 1kg on left & 49 kg on right, Similarly, for 153kg 153 =3x49 + 0x7 + 6x1 = 3x49 + 1x7 1x1 We can weigh 153 by putting 3 stones of 49kg & one 7kg stone on right and 1kg stone on left with the mushroom. The range of this will be 6x72+6x71+6x70=171. So, we can measure all weights till 171kg using only 3 kinds of stones : 1kg, 7kg & 49kg.
Similar Questions
Nkg−1 is the unit of :
01:36View SolutionA bag contains 100 identical marble stones which are numbered from 1 to 100. If one stone is drawn at random from the bag, find the probability that it bears a perfect square number.
01:42View SolutionA bag contains 100 identical marble stones which are numbered from 1 to 100. If one stone is drawn at random from the bag, find the probability that it bears a number divisible by 4.
03:09View SolutionA bag contains 100 identical marble stones which are numbered from 1 to 100. If one stone is drawn at random from the bag, find the probability that it bears :
(iii) a number divisible by 5.01:38View SolutionA bag contains 100 identical marble stones which are numbered from 1 to 100. If one stone is drawn at random from the bag, find the probability that it bears :
(iv) a number divisible by 4 or 5.01:03View SolutionA bag contains 100 identical marble stones which are numbered from 1 to 100. If one stone is drawn at random from the bag, find the probability that it bears :
(v) a number divisible by 4 and 5.01:01View SolutionA stone is weighed using a spring balance (Fig. C) and it weighs 40 g. But when it is dipped in water, it weighs only around 25 g. Why does it weigh less in water? Which force acting on the stone is responsible for this?
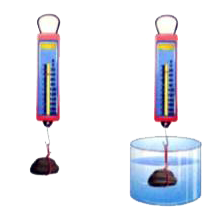 01:37View Solution
01:37View SolutionWho wanted to part with all the gold that he had and his precious stones?
View Solution

