To earn his wand, Harry was given 4 ropes and a lighter. Each rope burns at a non-con- stant rate but takes exactly one hour to burn completely from one end to the other. Harry can only light the ropes at either of their ends but can decide when to light each end as he sees fit. The goal is to use the ropes to measure time. For example, the time taken to burn one rope if burnt from only one end is 1 hour. So 1 hour can be measured using the ropes. Similarly, at max, how many lengths of time can be measured using these ropes? The right answer earns him his wand.
Step by step video & image solution for To earn his wand, Harry was given 4 ropes and a lighter. Each rope burns at a non-con- stant rate but takes exactly one hour to burn completely from one end to the other. Harry can only light the ropes at either of their ends but can decide when to light each end as he sees fit. The goal is to use the ropes to measure time. For example, the time taken to burn one rope if burnt from only one end is 1 hour. So 1 hour can be measured using the ropes. Similarly, at max, how many lengths of time can be measured using these ropes? The right answer earns him his wand. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A horse is tied to a rope of length 5 m and the other end of the rope is tied to a pole. Find the displacement and the distance travelled by the horse in the following cases.
When it makes one full revolution.
View SolutionA horse is tied to a rope of length 5 m and the other end of the rope is tied to a pole. Find the displacement and the distance travelled by the horse in the following cases: When it makes one full revolution.
View Solution
Knowledge Check
In figure the tension in the rope (rope is light) is
 A(M+m)gsinθB(M+m)gsinθ−μmgcosθCZeroD(M+m)gsinθ
A(M+m)gsinθB(M+m)gsinθ−μmgcosθCZeroD(M+m)gsinθA rope of mass M and length L is being rotated about one end in a gravity free space A pulse is being created at one of the ends.The angle through which rope will be rotated in the time when pulse reaches the opposite end of rope for first time end for the angular velocity of rope ω is
Aπ√2Bπ2Cπ2√2Dπ2A straight rope of length 'L' is kept on a frictionless horizontal surface and a force 'F' is applied to one end of the rope in the direction of its length and away from that end. The tension in the rope at a distance 'l' from that end is
AFlBLFlC(1−lL)FD(1+lL)F
A massless rope is strung over a frictionless pulley. A monkey holds onto one end of the rope, and a mirror, having the same weight as the monkey, is attached to the other end of the rope at the monkey's level.Can the monkey get away from its image seen in the mirror (a) by climbing up the rope,(b) by climbing down the rope, or (c) by releasing the rope ?
View SolutionA horse is tied to a rope of length 5 m and the other end of the rope is tied to a pole. Find the displacement and the distance travelled by the horse in the following cases.
When it makes 34 th of the revolution.
View SolutionA straight rope of length 'L' is kept on a frictionless horizontal surface and a force 'F' is applied to one end of the rope in the direction of its length and away from that end. The tension in the rope at a distance 'I from that end is 9
View SolutionOne end of a rope is fixed at a point on the ceiling the other end is held close to the first end so that the rope is folded. The second end is released from this position. Find the speed at which the fold at F is descending at the instant the free end of the rope is going down at speed V.
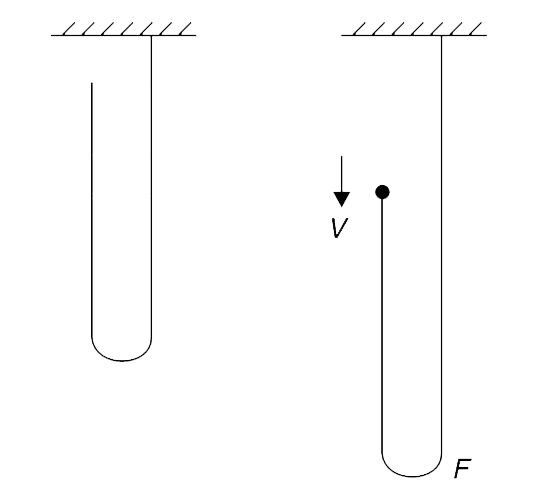
View SolutionWhat type of waves are illustrated by the movement of a rope whose one end is fixed to a pole and the other end is moved up and down?
View Solution
