A particle is projected from ground at some angle with horizontal (Assuming point of projection to the origin and the horizontal and vertical directions to be the x and y axis) the particle passes through the points (3, 4) m and (4, 3) m during its motion then the range of the particle would be : (g=10m/s2)
36 m
377 m
4 m
16 m
The correct Answer is:B
Step by step video & image solution for A particle is projected from ground at some angle with horizontal (Assuming point of projection to the origin and the horizontal and vertical directions to be the x and y axis) the particle passes through the points (3, 4) m and (4, 3) m during its motion then the range of the particle would be : (g=10 m//s^(2)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A particle is projected from origin at an angle is selected as X-axis and verticle as Y-axis . It is found that particle passes through the points (a, b) and (b, a). Calculate range and angle of projection .
View SolutionA particle is projected under gravity at an angle of projection 45∘ with horizontal. Its horizontal range is 36m. Find maximum Height attained by particle.
View Solution
Knowledge Check
A particle is projected from ground with velocity 3ˆi+4ˆi m/s. Find range of the projectile :-
A1.2mB3.6mC2.4mD10mA particle is projected from the ground with a kinetic energy E at an angle of 60° with the horizontal. Its kinetic energy at the highest point of its motion will be
AE/√2BE/2CE/4DE/8A particle is projected at angle θ with horizontal from ground. The slop (m) of the trajectory of the particle varies with time (t) as
A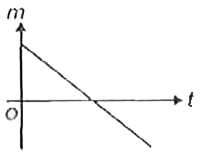 B
B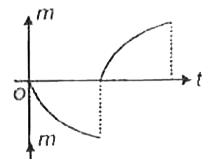 C
C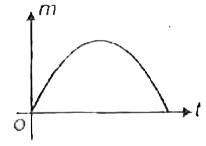 D
D
A body is projected from the ground with some speed at some angle with the horizontal. Taking the horizontal and vertical direction to be x and y axis respectively and the point of projection as origin, calculate the minimum speed (in ms−1) of projection so that it can pass through a point whose x and y coordinates are 30 m and 40 m respectively? Take g=10ms−2
View SolutionA particle is projected at an angle θ from ground with speed u (g = 10 m/s2 )
View SolutionA particle is projected at an angle θ with the horizontal . If angle of elevation of highest point of trajectory is ϕ when seen from point of projection, then
View SolutionA particle is projected with velocity 10m/s at an angle of 45∘ with the horizontal from some height. Consider point of projection as origin and motion in xy plane. Then (→g=10ˆjm/s2)
View SolutionA particle is projected from the ground . Point of projection is taken as origin, horizontal direction as X-axis and verticle upward direction ass Y-axis. Equation of trajectory of the partcle is y=αx−βx2. Horizontal range of the projectile is
View Solution
