Two linear simple harmonic motions of equal amplitude and frequency are impressed on a particle along x and y axis respectively. The initial phase difference between them is π2. The resultant path followed by the particle is
a circle
a straight line
an ellipse
a parabola
The correct Answer is:A
To solve the problem of the resultant path followed by a particle subjected to two linear simple harmonic motions (SHMs) along the x and y axes with a phase difference of π/2, we can follow these steps:
Step 1: Understand the Given Information
We are given two SHMs:
- Both have equal amplitude A and equal angular frequency ω.
- The first SHM is along the x-axis, and the second SHM is along the y-axis.
- The phase difference between the two SHMs is π2.
Step 2: Write the Equations of Motion
The equations for the two SHMs can be expressed as:
- For the x-axis:
x(t)=Asin(ωt)
- For the y-axis (with a phase difference of π2):
y(t)=Acos(ωt)
Step 3: Relate the Two Equations
We can express the sine and cosine functions in terms of each other:
- From the x-axis equation:
sin(ωt)=xA
- From the y-axis equation:
cos(ωt)=yA
Step 4: Use the Pythagorean Identity
Using the Pythagorean identity sin2(θ)+cos2(θ)=1:
(xA)2+(yA)2=1
Step 5: Rearranging the Equation
Multiplying through by A2 gives:
x2+y2=A2
Step 6: Identify the Resultant Path
The equation x2+y2=A2 represents a circle with:
- Center at the origin (0, 0)
- Radius A
Conclusion
The resultant path followed by the particle is a circular motion centered at the origin with a radius equal to the amplitude A.
We are given two SHMs:
- Both have equal amplitude A and equal angular frequency ω.
- The first SHM is along the x-axis, and the second SHM is along the y-axis.
- The phase difference between the two SHMs is π2.
The equations for the two SHMs can be expressed as:
- For the x-axis:
x(t)=Asin(ωt)
- For the y-axis (with a phase difference of π2):
y(t)=Acos(ωt)
We can express the sine and cosine functions in terms of each other:
- From the x-axis equation:
sin(ωt)=xA
- From the y-axis equation:
cos(ωt)=yA
Using the Pythagorean identity sin2(θ)+cos2(θ)=1:
(xA)2+(yA)2=1
Multiplying through by A2 gives:
x2+y2=A2
The equation x2+y2=A2 represents a circle with:
- Center at the origin (0, 0)
- Radius A
The resultant path followed by the particle is a circular motion centered at the origin with a radius equal to the amplitude A.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Advanced34videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - More than one option is correct50videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise 14.44videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct3videos
SEMICONDUCTORS AND ELECTRONIC DEVICES
- BOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)38videos
SOLVD PAPERS 2017 NEET, AIIMS & JIPMER
Similar Questions
Two linear SHM of equal amplitudes A and frequencies ω and 2ω are impressed on a particle along x and y−axes respectively. If the initial phase difference between them is π/2. Find the resultant path followed by the particle.
View SolutionTwo linear harmonic motions of equal amplitudes and frequencies ω and 2 ω imposed on a particle along the axes of x and y respectively. If the initial phase difference between them is π/2, then find the resultant path followed by the particle.
View Solution
Knowledge Check
- Question 1 - Select One
Two simple harmonic motions with the same frequency act on a particle at right angles i.e., along X-axis and Y-axis. If the two amplitudes are equal and the phase difference is π/2, the resultant motion will be
Aa circleBan ellipse with the major axis along Y-axisCan ellipse with the major axis along X-axisDa straight line inclined at 45∘ to the X-axis - Question 2 - Select One
When two mutually perpendicular simple harmonic motions of same frequency, amplitude and phase are susperimposed
Athe resulting motion is uniform circular motion.Bthe resulting motion is a linear simple harmonic motions along a straight ine inclined equally to the straight lines of motion of component ones.Cthe resulting motion is an elliptical motion, susmmetical about the lines of motion of the compounents.Dthe two S.H.M. will cancel each other. - Question 3 - Select One
When two particles performing SHM of same amplitude and frequency arriving at a point of medium simultaneously with phase difference of π/2, then the resultant path is
AparabolicBellipticalCcircleDstraight line
Two particles perform linear simple harmonic motion along the same path of length 2 A and period T as shown in the graph below. The phase difference between them is
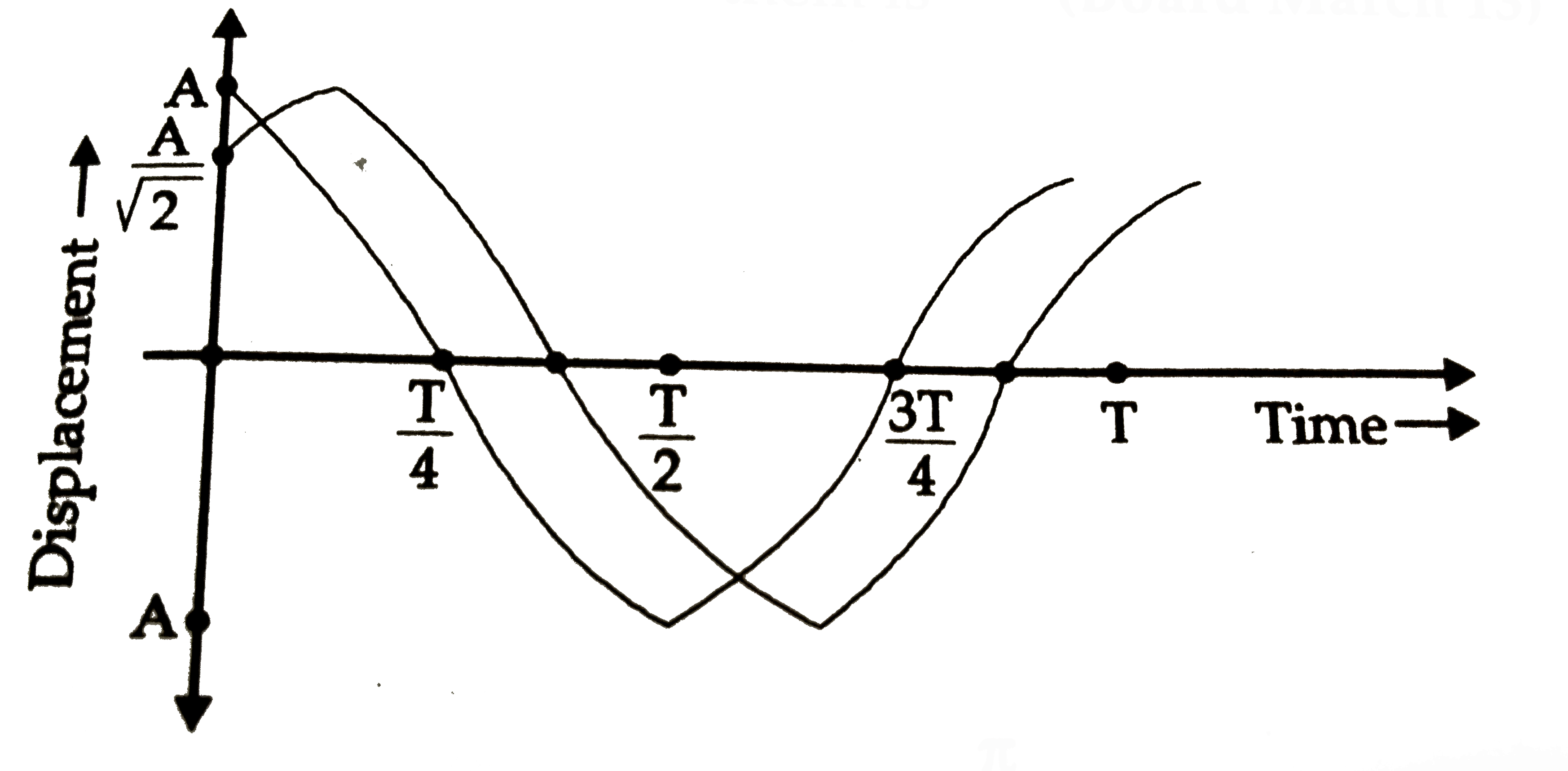 View Solution
View SolutionThe maximum seperation between two particles executing simple harmonic motion of the equal amplitude and same frequency along the same straight line and about the same mean position, is √3 times the amplitude of oscillation. IF the phase difference between them is ϕ, determine 2π/ϕ.
View SolutionA particle is subjected to two simple harmonic motion in the same direction having equal amplitudes and equal frequency. If the resultant amplitude is equal to the amplitude of the individual motions. Find the phase difference between the individual motions.
View SolutionTwo particles execute simple harmonic motion of the same amplitude and frequency along close parallel lines. They pass each other moving in opposite directions each time their displacement is half their amplitude. Their phase difference is
View SolutionTwo particles P and Q describe SHM of same amplitude a frequency ν along the same straight line. The maximum distance between two particles is √2a. The initial phase difference between the particles is
View Solution

