The electric dipoles of moments p1andp2 are in a straight line. Show that the potential energy of each in the presence of the other is −12πε0⋅p1p2r3, where r is the distance between the dipoles. (Assume r to be much greater than the length of the dipole).
Step by step video & image solution for The electric dipoles of moments p_(1) and p_(2) are in a straight line. Show that the potential energy of each in the presence of the other is -(1)/(2piepsi_(0))*(p_(1)p_(2))/(r^(3)), where r is the distance between the dipoles. (Assume r to be much greater than the length of the dipole). by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - ELECTRIC POTENTIAL AND ELECTRIC FLUXEXERCISE - Problem15videos
ELECTRIC POTENTIAL AND ELECTRIC FLUX
- BOOK - SL ARORACHAPTER - ELECTRIC POTENTIAL AND ELECTRIC FLUXEXERCISE - Problems for self practive61videos
ELECTRIC POTENTIAL AND ELECTRIC FLUX
- BOOK - SL ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - Problems For Self101videos
CURRENT ELECTRICITY
- BOOK - SL ARORACHAPTER - ELECTRICAL INSTRUMENTSEXERCISE - Problem for self practice81videos
ELECTRICAL INSTRUMENTS
Similar Questions
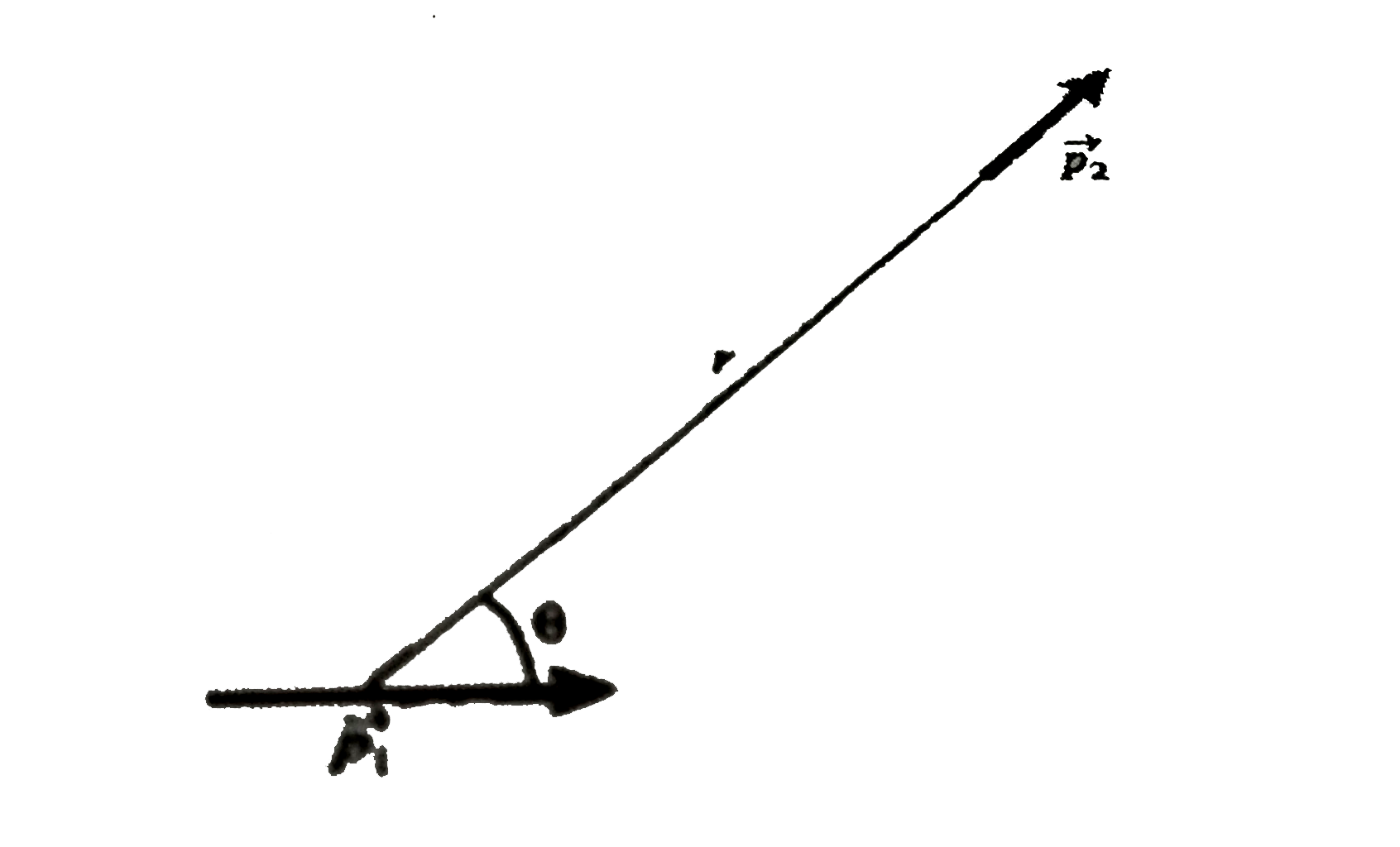
Two short electric dipoles are placed as shown in figure. Find the potential energy of electric interaction between these dipoles.
[−Kp1p2cosθr3]
 View Solution
View SolutionTwo identical electric point dipoles have dipole moments −→P1=pˆiand−→P2=pˆi and are held on the x axis at distance 'a' from each other. When released, they move along the x-axis with the direaction of their dipole moments remaining unchanged. If the mass of each dipole is 'm', their speed when they are infinitely for apart is :
View Solution
Knowledge Check
- Question 1 - Select One
Two point dipoles of dipole moment →p1and→p2 are at a distance x from each other and →p1∣∣→p2 . The force between the dipoles is :
A14πε04p1p2x4B14πε03p1p2x3C14πε06p1p2x4D14πε08p1p2x4 - Question 2 - Select One

Two point electric dipoles with dipole moment P1 and P2 are separated by a distance r with their dipole axes mutually perpendicular as shown. The force of interaction between the dipoles is (where k=14πε0)A2kP1P2r4B3kP1P2r3C4kP1P2r4D6kP1P2r4 - Question 3 - Select One
When dipole moment →p of a dipole is parallel to electric field intensity →E (stable equilibrium) the potential energy of dipole is
Apositive, maximumBpositve, minimumCnegative, maximumDnegative, minimum
An electric dipole of moment p is kept at a distance r form an infinte long charged wire of linear charge density λ as shown.Find the force acting on the dipole?
 View Solution
View SolutionTwo short electric dipoles of moment P and 8P are placed in opposite direction on a line at a distance of 15cm.The electric field will be zero at point between the dipoles whose distance from the dipole of moment P is?
View SolutionA short electric dipole has dipole moment p. Find the distance of farthest point from the dipole where (a) potential due to the dipole is V0 (b) Electric field due to the dipole is E0
View SolutionTwo electric dipoles of moment p and 64p are placed in opposite direction on a line at a distance of 25cm. The electric field will be zero at point between the dipoles whose distance from the dipole of moment p is
View SolutionA dipole of electric dipole moment p is placed in a uniform electric field of strength E. If θ is the angle between positive direction of p and E, then the potential energy of the electric dipole is largest when θ is
View Solution

