How will you connected four capacitors, each of capacitance 1μF to obtain a net capacitance of 0.75μF? Draw a diagram to show the combination
To achieve a net capacitance of 0.75 µF using four capacitors, each with a capacitance of 1 µF, we can connect them in a combination of series and parallel. Here’s how to do it step by step:
1. Understanding the Configuration:
- We have 4 capacitors, each with a capacitance of 1 µF.
- We need to find a way to connect them to achieve a total capacitance of 0.75 µF.
2. Assuming Capacitors in Series and Parallel:
- Let's assume we connect X capacitors in series and the remaining 4−X capacitors in parallel.
3. Capacitance of Capacitors in Series:
- The formula for the total capacitance \( C_s \) of capacitors in series is given by:
\(
\frac{1}{C_s} = \frac{1}{C_1} + \frac{1}{C_2} + \ldots + \frac{1}{C_X}
\)
- Since all capacitors have the same capacitance (1 µF), this simplifies to:
\(
C_s = \frac{1}{X} \text{ µF}
\)
4. Capacitance of Capacitors in Parallel:
- The capacitance \( C_p \) of capacitors in parallel is given by:
\(
C_p = C_1 + C_2 + \ldots + C_{4-X} = (4 - X) \times 1 \text{ µF} = (4 - X) \text{ µF}
\)
5. Total Capacitance of the Combination:
- The total capacitance \( C_{total} \) of the combination of series and parallel is given by:
\(
C_{total} = C_s + C_p
\)
- Since \( C_s \) is in series with \( C_p \):
\(
C_{total} = \frac{1}{X} + (4 - X)
\)
6. Setting Up the Equation:
- We want \( C_{total} = 0.75 \) µF:
\(
\frac{1}{X} + (4 - X) = 0.75
\)
7. Solving the Equation:
- Rearranging gives:
\(
\frac{1}{X} = 0.75 - (4 - X)
\)
\(
\frac{1}{X} = X - 3.25
\)
- Multiplying both sides by \( X \):
\(
1 = X^2 - 3.25X
\)
- Rearranging gives:
\(
X^2 - 3.25X - 1 = 0
\)
8. Using the Quadratic Formula:
- Applying the quadratic formula \( X = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \):
\(
X = \frac{3.25 \pm \sqrt{(3.25)^2 + 4}}{2}
\)
- Solving this gives two possible values for \( X \). However, since \( X \) must be a whole number, we find \( X = 1 \).
9. Final Configuration:
- Thus, we connect 1 capacitor in series and 3 capacitors in parallel.
Diagram
±−−(1µF)−−−+∣∣||∣||(1µF)(1µF)∣∣∣±−−(1µF)−−−+
Summary
- Connect 1 capacitor in series with the combination of 3 capacitors in parallel to achieve a net capacitance of 0.75 µF.
- We have 4 capacitors, each with a capacitance of 1 µF.
- We need to find a way to connect them to achieve a total capacitance of 0.75 µF.
- Let's assume we connect X capacitors in series and the remaining 4−X capacitors in parallel.
- The formula for the total capacitance \( C_s \) of capacitors in series is given by:
\(
\frac{1}{C_s} = \frac{1}{C_1} + \frac{1}{C_2} + \ldots + \frac{1}{C_X}
\)
- Since all capacitors have the same capacitance (1 µF), this simplifies to:
\(
C_s = \frac{1}{X} \text{ µF}
\)
- The capacitance \( C_p \) of capacitors in parallel is given by:
\(
C_p = C_1 + C_2 + \ldots + C_{4-X} = (4 - X) \times 1 \text{ µF} = (4 - X) \text{ µF}
\)
- The total capacitance \( C_{total} \) of the combination of series and parallel is given by:
\(
C_{total} = C_s + C_p
\)
- Since \( C_s \) is in series with \( C_p \):
\(
C_{total} = \frac{1}{X} + (4 - X)
\)
- We want \( C_{total} = 0.75 \) µF:
\(
\frac{1}{X} + (4 - X) = 0.75
\)
- Rearranging gives:
\(
\frac{1}{X} = 0.75 - (4 - X)
\)
\(
\frac{1}{X} = X - 3.25
\)
- Multiplying both sides by \( X \):
\(
1 = X^2 - 3.25X
\)
- Rearranging gives:
\(
X^2 - 3.25X - 1 = 0
\)
- Applying the quadratic formula \( X = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \):
\(
X = \frac{3.25 \pm \sqrt{(3.25)^2 + 4}}{2}
\)
- Solving this gives two possible values for \( X \). However, since \( X \) must be a whole number, we find \( X = 1 \).
- Thus, we connect 1 capacitor in series and 3 capacitors in parallel.
±−−(1µF)−−−+∣∣||∣||(1µF)(1µF)∣∣∣±−−(1µF)−−−+
- Connect 1 capacitor in series with the combination of 3 capacitors in parallel to achieve a net capacitance of 0.75 µF.
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - CAPACITORSEXERCISE - Problem From Competitive Examinations17videos
CAPACITORS
- BOOK - SL ARORACHAPTER - CAPACITORSEXERCISE - problem for self practive65videos
CAPACITORS
- BOOK - SL ARORACHAPTER - ATOMS, NUCLEI AND MOLECULESEXERCISE - Problems For Self Practice87videos
ATOMS, NUCLEI AND MOLECULES
- BOOK - SL ARORACHAPTER - CHEMICAL EFFECT OF CURRENTEXERCISE - TYPE-B5videos
CHEMICAL EFFECT OF CURRENT
Similar Questions
A network of four capacitors, each of capacitance 15μF,is connected across a battery of 100 V as shown in the figure. Find the net capacitance and the charge on the capacitor C4.
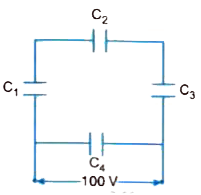 View Solution
View SolutionSeven capacitors each of capacitance 2μF are to be connected in a configuration to obtain an effective capacitance of (1011)μF. Which of the combination (s) shown in figure will achieve the desired result?
View Solution
Knowledge Check
- Question 1 - Select One
Minimum number of capacitors of 2μF capacitance each required to obtain a capacitor of 5μF will be
AThreeBFourCFiveDSix - Question 2 - Select One
Minimum number of capacitors of 4μF capacitance each required to obtain a capacitor of 10μF will be
A3B4C5D6 - Question 3 - Select One
The minimum number of condensers each capacitance of 2μF, in order to obtain result capacitance of 5μF will be
A4B5C6D3
Seven capacitors each of capacitance 2μF are to be connected in a configuration to obtain an effective capacitance of (1011)μF. Which of the combination (s) shown in figure will achieve the desired result?
View SolutionHow do you arrange four equal capacitor of 4μF to get effective capacitance 3μF ?
View SolutionFour capacitors, each of capacitance 4μF, are connected as shown here. The equivalent capacitance between the points A and B will be
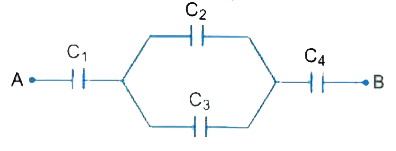 View Solution
View SolutionConnect three capacitors of 3μF,3μF and 6μF such that their equivalent capacitance is 5μF.
View SolutionTwo capacitors of capacitances 3μFand5μF respectively are connected in parallel and this combination is connected in series with a third capacitor of capacitance 2μF. A potential difference of 100 V is applied across the entire combination. The charge and the potential difference across the third capacitor is
View Solution

