A solid sphere of radius R and mass M is rolled by a force F acting at the top of the sphere as shown in the figure. The sphere starts from rest and rolls without slipping, then
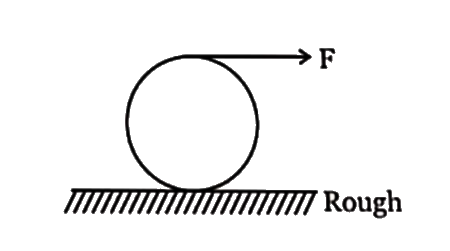
work done by force F when the centre moves a distance S is 2 FS
work done by force F when the centre moves a distance S is 3 FS
work done by force F when the center moves a distance S is FS
work done by force F when the center moves a distance S is 4FS
The correct Answer is:A
Step by step video & image solution for A solid sphere of radius R and mass M is rolled by a force F acting at the top of the sphere as shown in the figure. The sphere starts from rest and rolls without slipping, then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is

View Solution
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View Solution
Knowledge Check
A solid sphere of radius R is rolled by a force F acting at the topo of the sphere as shown in the figure. There is no slipping and initially sphere is in the rest position, then (CM= centre of mass)
 AWork done by force F when the centre of mass move a distance S is 2 FSBspeed of the CM when CM moves a distance S is √207FSMCwork done by the Force F when CM move a distance S is FSDspeed of the CM when CM moves a distance S is √65FSM
AWork done by force F when the centre of mass move a distance S is 2 FSBspeed of the CM when CM moves a distance S is √207FSMCwork done by the Force F when CM move a distance S is FSDspeed of the CM when CM moves a distance S is √65FSM
A uniform solid cylinder having mass M and radius R is pulled by a horiozntal force F acting through the center as shown. The cylinder rolls to the right without slipping. What is the magnitude of the force of friction between the cylinder and the ground?AF/4BF/3CF/2D2F/3A small sphere S of radius ,r and mass m rolls without slipping, inside a large hemispherical bowl B of radius R as shown in figure. S starts from rest at the top point of the hemisphere
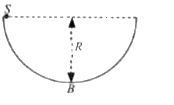 AThe fraction of translational kinetic energy at the sphere is 5/7.BThe fraction of rotational kinetic energy of the sphere is 2/7.CThe fraction of rotational kinetic energy of the sphere is 27mv2.DThe total kinetic energy of the sphere at the bottom of the bowl is 27mv2
AThe fraction of translational kinetic energy at the sphere is 5/7.BThe fraction of rotational kinetic energy of the sphere is 2/7.CThe fraction of rotational kinetic energy of the sphere is 27mv2.DThe total kinetic energy of the sphere at the bottom of the bowl is 27mv2
A solid sphere of mass M and radius R is covered with a thin shell of mass M. There is no friction between the inner wall of the shell and the sphere. The ball is released from rest, and then it rolls without slipping down an incline that is inclined at an angle θ to the horizontal. Find the acceleration of the ball.
View Solution
A tangential force F acts at the top of a thin spherical shell of mass m and radius R. Find the acceleration of the shell if it rolls without slipping.
View Solution
A solid sphere of mass M and radius R is hit by a cue at a height h above the centre C. for what value of h the sphere will rool without slipping ?
View SolutionA uniform solid sphere of radius r=R5 is placed on the inside surface of a hemisherical bowl with radius R(=5r). The sphere is released from rest at an angle θ=37∘ to the vertical and rolls without slipping (Fig.) The angular speed of the sphere when it reaches the bottom of the bowl is.
 .
.
View SolutionA small sphere D of mass and radius rols without slipping inside a large fixed hemispherical radius R(>>r) as shown in figure. If the sphere starts from rest at the top point of the hemisphere normal force exerted by the small sphere on the hemisphere when its is at the bottom B of the hemisphere.
 .
.
View Solution
